2022-2023学年广东省佛山市顺德区卓越高中联考高二（上）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．直线

  x

  3

  +

  y

  3

  =

  1

  的倾斜角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：204引用：10难度：0.9

  解析

• 2．以点A（1，2）为圆心，两平行线x-y+1=0与2x-2y+7=0之间的距离为半径的圆的方程为（　　）

  A．（x+1）²+（y+2）²= 9 2	B．（x-1）²+（y-2）²= 25 8
  C．（x+1）²+（y+2）²= 25 8	D．（x-1）²+（y-2）²= 9 2
  组卷：180引用：12难度：0.7

  解析

• 3．甲、乙两队进行篮球比赛，采取五场三胜制（当一队得三场胜利时，该队获胜，比赛结束），根据前期比赛成绩，甲队的主客场安排依次为“主主客客主”．设甲队主场取胜的概率为0.6，客场取胜的概率为0.3；且各场比赛结果相互独立，则甲队以3：1获胜的概率是（　　）

  A．0.0972

  B．0.1188

  C．0.0756

  D．0.0216
  组卷：31引用：4难度：0.7

  解析

• 4．已知平面α={P|

  n

  •

  P

  0

  P

  =0}，其中点P₀（1，2，3），法向量

  n

  =（1，1，1），则下列各点中不在平面α内的是（　　）

  A．（3，2，1）

  B．（-2，5，4）

  C．（-3，4，5）

  D．（2，-4，8）
  组卷：724引用：15难度：0.8

  解析

• 5．设x,y∈R，向量

  a

  =

  （

  x

  ,

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  y

  ,

  1

  ）

  ，

  c

  =

  （

  1

  ，-

  1

  ，

  1

  ）

  ，且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，则

  |

  a

  +

  b

  |

  =（　　）

  A． 5

  B．3

  C． 2 2

  D．4
  组卷：32引用：4难度：0.7

  解析

• 6．已知两点A（-3，4），B（3，2），过点P（1，0）的直线l与线段AB有公共点，则直线l的斜率k的取值范围是（　　）

  A．（-1，1）	B．（-∞，-1）∪（1，+∞）
  C．[-1，1]	D．（-∞，-1]∪[1，+∞）
  组卷：2086引用：23难度：0.9

  解析

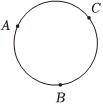• 7．如图，一动点沿圆周在均匀分布的A，B，C三点之间移动，每次该动点逆时针方向移动的概率是顺时针方向移动概率的两倍，假设现在该点从A点出发，则移动三次之后到达B点的概率是（　　）

  A． 4 27

  B． 2 9

  C． 4 9

  D． 8 27
  组卷：7引用：2难度：0.8

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

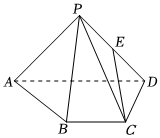• 21．如图，在四棱锥P-ABCD中，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，平面PAD⊥平面ABCD，BC=CD=1，底面ABCD的面积为

  3

  2

  ，E为PD的中点．
  （1）证明：CE∥平面PAB；
  （2）求点A到直线CE的距离；
  （3）求直线CE与平面PAB间的距离．
  组卷：23引用：2难度：0.6

  解析

• 22．如图1是一个正方形和一副直角三角板（常用的文具），其中AD=A₁D₁=B₁C₁=M₂D₁=2，B₁M₁=4，将AD与A₁D₁、BC与B₁C₁分别重合，并将两个三角板翻起，使点M₁与点M₂重合于点M，得到一几何体如图2．
  
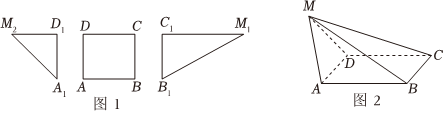
  （1）证明：AD⊥MC；
  （2）求平面MAD与平面MBC的夹角的余弦值；
  （3）在正方形ABCD范围内有以圆心为D、半径为2的一段圆弧，则在该段圆弧上，是否存在点N，使得直线MC与直线DN所成角为

  π

  4

  ？试说明你的理由．
  组卷：13引用：2难度：0.6

  解析