如图1是一个正方形和一副直角三角板（常用的文具），其中AD=A1D1=B1C1=M2D1=2，B1M1=4，将AD与A1D1、BC与B1C1分别重合，并将两个三角板翻起，使点M1与点M2重合于点M，得到一几何体如图2．
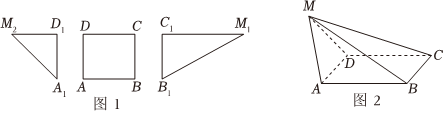
（1）证明：AD⊥MC；
（2）求平面MAD与平面MBC的夹角的余弦值；
（3）在正方形ABCD范围内有以圆心为D、半径为2的一段圆弧，则在该段圆弧上，是否存在点N，使得直线MC与直线DN所成角为π4？试说明你的理由．
π
4
【答案】（1）证明见解析．
（2）．
（3）存在符合题意的点N，理由见解析．
（2）
3
2
（3）存在符合题意的点N，理由见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/24 4:0:8组卷：13引用：2难度：0.6
相似题
-
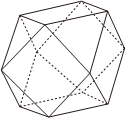1．“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为（ ）发布：2024/11/9 21:30:1组卷：173引用：3难度：0.5 -
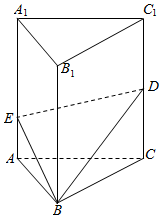2．如图，三棱柱ABC-A1B1C1满足棱长都相等且AA1⊥平面ABC，D是棱CC1的中点，E是棱AA1上的动点．设AE=x,随着x增大，平面BDE与底面ABC所成锐二面角的平面角是（ ）发布：2024/12/11 21:0:1组卷：1630引用：12难度：0.3 -
3．如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC=2，BC=CC1=4，点D是棱AB的中点，则平面ABB1A1与平面B1CD所成角的正弦值为（ ）发布：2024/11/15 14:30:2组卷：446引用：2难度：0.6
