2022-2023学年新疆喀什地区伽师县高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．在空间直角坐标系Oxyz中，已知A（-1，0，0），B（1，2，-2），C（0，0，-2），D（2，2，-4），则以下错误的是（　　）

  A． AC • AB = 6

  B． AC ， AB 夹角的余弦值为 15 6

  C．A，B，C，D共面

  D．点O到直线AB的距离是 6 3
  组卷：101引用：6难度：0.7

  解析

• 2．已知点A（1，

  3

  ），B（-1，3

  3

  ），则直线AB的倾斜角是（　　）

  A． π 3

  B． π 6

  C． 2 π 3

  D． 5 π 6
  组卷：49引用：11难度：0.9

  解析

• 3．若椭圆

  y

  2

  16

  +

  x

  2

  4

  =1上一点A到焦点F₁的距离为3，则点A到焦点F₂的距离为（　　）

  A．6

  B．5

  C．4

  D．3
  组卷：17引用：2难度：0.7

  解析

• 4．已知P，Q分别是直线l：x-y-2=0和圆C：x²+y²=1上的动点，圆C与x轴正半轴交于点A（1，0），则|PA|+|PQ|的最小值为（　　）

  A． 2

  B．2

  C． 5 - 1

  D． 2 + 10 2 -1
  组卷：108引用：9难度：0.7

  解析

• 5．已知椭圆

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  ，双曲线

  C

  2

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  ，其中a＞b＞0．若C₁与C₂的焦距之比为1：3，则C₂的渐近线方程为（　　）

  A． 2 x ± 5 y = 0

  B． 5 x ± 2 y = 0

  C． x ± 2 y = 0

  D． 2 x ± y = 0
  组卷：332引用：6难度：0.7

  解析

• 6．已知a,b都是实数，那么“a＞2”是“方程x²+y²-2x-a=0表示圆”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：153引用：5难度：0.8

  解析

• 7．三棱柱ABC-A₁B₁C₁中，记

  BA

  =

  a

  ，

  B

  B

  1

  =

  b

  ，

  BC

  =

  c

  ，则

  C

  1

  A

  =（　　）

  A．- a + b + c

  B． a + b - c

  C． a - b - c

  D． a + b + c
  组卷：2引用：2难度：0.8

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．如图，四棱锥P-ABCD的底面是平行四边形，AD=2AB=6，

  PA

  =

  PD

  =

  3

  2

  ，PD⊥AB，AC=BD，点M在侧棱PD上，且PD=3MD．
  （1）证明：平面PAB⊥平面PAD；
  （2）求平面PAB与平面MAC所成锐二面角的余弦值．
  组卷：101引用：3难度：0.6

  解析

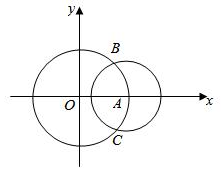• 22．如图，在平面直角坐标系xOy中，圆O：x²+y²=4与x轴的正半轴交于点A，以点A为圆心的圆A：（x-2）²+y²=r²（r＞0）与圆O交于B，C两点．
  （1）当r=

  2

  时，求BC的长；
  （2）当r变化时，求

  AB

  •

  AC

  的最小值；
  （3）过点P（6，0）的直线l与圆A切于点D，与圆O分别交于点E，F，若点E是DF的中点，试求直线l的方程．
  组卷：163引用：3难度：0.6

  解析