2021-2022学年江苏省常州市溧阳中学高一（上）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设集合A={x|-2＜x＜4}，B={2，3，4，5}，则A∩B=（　　）

  A．{2}

  B．{2，3}

  C．{3，4}

  D．{2，3，4}
  组卷：267引用：24难度：0.7

  解析

• 2．命题“∀x∈R，x²≥0”的否定为（　　）

  A．∀x∈R，x2＜0	B．不存在x∈R，x2＜0
  C．∃x∈R，x2≥0	D．∃x∈R，x2＜0
  组卷：25引用：3难度：0.8

  解析

• 3．二次函数y=ax²+bx+c的部分对应值如下表：
  

  x	-3	-2	-1	0	1	2	3	4
  y	6	0	-4	-6	-6	-4	0	6

  则不等式ax²+bx+c＞0的解集为（　　）

  A．（-2，3）	B．（-3，2）
  C．（-∞，-2）∪（3，+∞）	D．（-∞，-3）∪（2，+∞）
  组卷：2引用：1难度：0.7

  解析

• 4．已知f（x）是定义在[a,b]上的函数，那么“函数f（x）在[a,b]上单调递增”是“函数f（x）在[a,b]上的最小值为f（a）”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：8引用：2难度：0.7

  解析

• 5．设m＞0，n＞0，且2m+5n=20，则mn的最大值为（　　）

  A． 10

  B． 2 10

  C．10

  D．20
  组卷：37引用：3难度：0.8

  解析

• 6．若3^x=5^y=k,且

  1

  x

  +

  1

  y

  =

  2

  ，则k的值为（　　）

  A． 2 2

  B． 15

  C．15

  D．225
  组卷：15引用：1难度：0.7

  解析

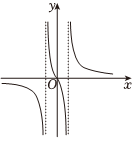• 7．在数学中，常用函数图象来研究函数性质，也常用函数解析式来分析函数图象的特征．已知函数f（x）的部分图象如图所示，则函数f（x）的解析式可能为（　　）

  A． f （ x ） = 2 x x 2 - 1	B． f （ x ） = 2 x x 2 + 1
  C． f （ x ） = 2 x 1 - | x |	D． f （ x ） = x 2 + 1 x 2 - 1
  组卷：12引用：1难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．为防止未成年人沉迷网络游戏，切实保护未成年人身心健康，2021年8月30日，国家新闻出版署下发《关于进一步严格管理切实防止未成年人沉迷网络游戏的通知》，通知要求：“严格限制向未成年人提供网络游戏服务的时间，所有网络游戏企业仅可在周五，周六，周日和法定节假日每日20时至21时向未成年人提供1小时服务，其他时间均不得以任何形式向未成年人提供网络游戏服务．”为落实上述通知要求，某网络游戏企业对新出品的一款游戏没定了“防沉迷系统”，规则如下：
  ①0到45分钟（不含0，含45分钟）为正常游戏时间，玩家在这段时间内获得的累积经验值E与游戏时间t（分钟）满足关系式：

  E

  =

  1

  9

  t

  2

  +

  4

  t

  +

  a

  ；
  ②45到55分钟（含55分钟）为视力疲劳时间，玩家在这段时间内获得的经验值为0（即累积经验值不变）；
  ③55到60分钟（含60分钟）为下线提醒时间，累积经验值开始减少，玩家每多玩1分钟，累积经验值将减少64；
  ④1小时后，无论玩家是否退出游戏，平台都将自动关闭．
  （1）当a=15时，求出累积经验值E与游戏时间t（0＜t≤60）的函数关系式E=f（t）；
  （2）该游戏企业把累积经验值E与游戏时间t的比值称为“玩家愉悦指数”，记作H（t），若a＞0且该游戏企业希望在正常游戏时间内，这款游戏的“玩家愉悦指数”不低于6，求a的最小值．
  组卷：53引用：3难度：0.6

  解析

• 22．设二次函数f（x）=ax²+bx+1（a＞0）．
  （1）若x₁，x₂是函数f（x）的两个零点（x₁＜x₂），且f（x）最小值为-a.
  ①求证：x₂-x₁=2；
  ②当且仅当a在什么范围内时，函数g（x）=f（x）+2x在区间（x₁，x₂）上存在最小值？
  （2）若任意实数t,在闭区间[t-2，t+2]上总存在两实数m,n,使得|f（m）-f（n）|≥2021成立，求实数a的取值范围．
  组卷：52引用：2难度：0.6

  解析