为防止未成年人沉迷网络游戏，切实保护未成年人身心健康，2021年8月30日，国家新闻出版署下发《关于进一步严格管理切实防止未成年人沉迷网络游戏的通知》，通知要求：“严格限制向未成年人提供网络游戏服务的时间，所有网络游戏企业仅可在周五，周六，周日和法定节假日每日20时至21时向未成年人提供1小时服务，其他时间均不得以任何形式向未成年人提供网络游戏服务．”为落实上述通知要求，某网络游戏企业对新出品的一款游戏没定了“防沉迷系统”，规则如下：
①0到45分钟（不含0，含45分钟）为正常游戏时间，玩家在这段时间内获得的累积经验值E与游戏时间t（分钟）满足关系式：E=19t2+4t+a；
②45到55分钟（含55分钟）为视力疲劳时间，玩家在这段时间内获得的经验值为0（即累积经验值不变）；
③55到60分钟（含60分钟）为下线提醒时间，累积经验值开始减少，玩家每多玩1分钟，累积经验值将减少64；
④1小时后，无论玩家是否退出游戏，平台都将自动关闭．
（1）当a=15时，求出累积经验值E与游戏时间t（0＜t≤60）的函数关系式E=f（t）；
（2）该游戏企业把累积经验值E与游戏时间t的比值称为“玩家愉悦指数”，记作H（t），若a＞0且该游戏企业希望在正常游戏时间内，这款游戏的“玩家愉悦指数”不低于6，求a的最小值．
E
=
1
9
t
2
+
4
t
+
a
【答案】（1）E=f（t）=
．
（2）9．
1 9 t 2 + 4 t + 15 ， 0 ＜ t |
420 ， 45 ＜ t ≤ 55 |
- 64 t + 3490 ， 55 ＜ t ≤ 60 |
（2）9．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/3 3:0:9组卷：53引用：3难度：0.6
相似题
-
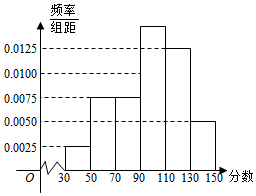1．某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于90分的具有复赛资格，某校有800名学生参加了初赛，所有学生的成绩均在区间（30，150]内，其频率分布直方图如图．
（Ⅰ）求获得复赛资格的人数；
（Ⅱ）从初赛得分在区间（110，150]的参赛者中，利用分层抽样的方法随机抽取7人参加学校座谈交流，那么从得分在区间（110，130]与（130，150]各抽取多少人？
（Ⅲ）从（Ⅱ）抽取的7人中，选出3人参加全市座谈交流，设X表示得分在区间（130，150]中参加全市座谈交流的人数，求X的分布列及数学期望E（X）．发布：2024/12/29 13:30:1组卷：134引用：7难度：0.5 -
2．设离散型随机变量X的分布列如表：
若离散型随机变量Y=-3X+1，且E（X）=3，则（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 发布：2024/12/29 13:0:1组卷：199引用：6难度：0.5 -
3．从4名男生和2名女生中任选3人参加演讲比赛，用X表示所选3人中女生的人数，则E（X）为（ ）
发布：2024/12/29 13:30:1组卷：139引用：6难度：0.7
