2023年江西省鹰潭市高考数学一模试卷（理科）

一、选择题：本大题共12个小题，每小题5分，共60分

• 1．已知集合A={x|y=ln（x-1）}，集合B={x|x²-2x＜0}，则A∩B=（　　）

  A．{x|x＞1}

  B．{x|0＜x＜2}

  C．{x|1＜x＜2}

  D．{x|0＜x≤2}
  组卷：61引用：2难度：0.7

  解析

• 2．已知复数

  z

  1

  +

  i

  为纯虚数，且

  |

  z

  1

  +

  i

  |

  =

  1

  ，则z=（　　）

  A．1-i

  B．1+i

  C．-1+i或1-i

  D．-1-i或1+i
  组卷：81引用：3难度：0.7

  解析

• 3．设a为实数，直线l₁：ax+y=1，直线l₂：x+ay=2a,则“a≠-1”是“l₁，l₂不平行”的（　　）条件

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：41引用：2难度：0.7

  解析

• 4．公差不为0的等差数列{a_n}满足：

  a

  2

  3

  +

  a

  2

  4

  =

  a

  2

  5

  +

  a

  2

  6

  ，S_n为数列{a_n}的前n项和，则（　　）

  A．a4=0

  B．a5=0

  C．S8=0

  D．S9=0
  组卷：87引用：1难度：0.7

  解析

• 5．已知

  0

  ＜

  α

  ＜

  π

  2

  ，

  sin

  （

  2

  α

  -

  π

  6

  ）

  =

  -

  1

  3

  ，则

  sin

  （

  α

  +

  π

  6

  ）

  =（　　）

  A． 3 3

  B． - 3 3

  C． 6 3

  D． - 6 3
  组卷：204引用：5难度：0.7

  解析

• 6．斐波那契数列{F_n}因数学家莱昂纳多•斐波那契（LeonardodaFibonaci）以兔子繁殖为例而引入，故又称为“兔子数列”．因n趋向于无穷大时，

  F

  n

  F

  n

  +

  1

  无限趋近于黄金分割数，也被称为黄金分割数列．在数学上，斐波那契数列由以下递推方法定义：数列{F_n}满足F₁=F₂=1，F_n+2=F_n+1+F_n，若从该数列前10项中随机抽取2项，则抽取的2项至少有1项是奇数的概率为（　　）

  A． 1 15

  B． 13 15

  C． 2 15

  D． 14 15
  组卷：35引用：1难度：0.7

  解析

• 7．已知实数x,y满足

  x + y - 1 ≤ 0

  x - y + 1 ≥ 0

  y ≥ - 1

  ，则

  z

  =

  x

  +

  2

  y

  -

  7

  y

  -

  2

  的最小值为（　　）

  A． 7 3

  B．3

  C． 11 3

  D．5
  组卷：46引用：2难度：0.6

  解析

三、解答题：共70分。解答应写出必要的文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

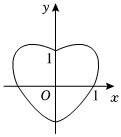• 22．数学中有许多美丽的曲线，如在平面直角坐标系xOy中，曲线E：

  x

  2

  +

  y

  2

  =

  a

  （

  x

  2

  +

  y

  2

  -

  y

  ）

  （

  a

  ＞

  0

  ）

  的形状如心形（如图），称这类曲线为心形曲线．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，当a=2时，
  （1）求E的极坐标方程；
  （2）已知P，Q为曲线E上异于O的两点，且

  OP

  •

  OQ

  =

  0

  ，求△OPQ的面积的最大值．
  组卷：219引用：7难度：0.6

  解析

• 23．已知m≥0，函数f（x）=2|x-1|-|2x+m|的最大值为4，
  （1）求实数m的值；
  （2）设正数x,y,z满足2x+2y+z=m,求3xy+yz+zx的最大值．
  组卷：23引用：1难度：0.4

  解析