当前位置：试卷中心 > 试卷详情

2022-2023学年河南省实验中学高一（下）期中数学试卷

发布：2024/8/29 2:0:8

一、单选题（本大题共8小题，每小题5分，共40分。）

1．如果直线a⊂平面α，直线b⊂平面β，且α∥β，则a与b的位置关系为（　　）
A．共面 B．平行 C．异面 D．平行或异面
组卷：194引用：3难度：0.9
解析
2．若复数z满足（1+i）²z=3+4i,则在复平面内z的共轭复数所对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：187引用：5难度：0.8
解析
3．已知
|
b
|
=
3
，且
a
•
b
=
-
2
，则向量
a
在向量
b
上的投影向量为（　　）
A．
-
2
3
a
B．
2
3
a
C．
-
2
3
b
D．
2
3
b
组卷：455引用：3难度：0.6
解析
4．攒尖是古代中国建筑中屋顶的一种结构形式，依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，多见于亭阁式建筑．如故宫中和殿的屋顶为四角攒尖顶，它的主要部分的轮廓可近似看作一个正四棱锥，设正四棱锥的侧面等腰三角形的顶角为60°，则该正四棱锥的侧面积与底面积的比为（　　）
A．
3
4
B．
3
3
C．
3
2
D．
3
组卷：220引用：6难度：0.6
解析
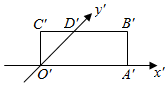5．如图所示，矩形O'A'B'C'是一个水平放置的平面图形的直观图，其中O'A'=3，O'C'=1，则原图形是（　　）
A．面积为
6
2
的菱形 B．面积为
6
2
的矩形
C．面积为
3
2
4
的菱形 D．面积为
3
2
4
的矩形
组卷：357引用：8难度：0.7
解析
6．在△ABC中，角A，B，C所对的边分别为a,b,c,已知A=60°，
b
=
2
3
，为使此三角形有两个，则a满足的条件是（　　）
A．
3
＜
a
＜
3
B．
3
＜
a
＜
2
3
C．
3
＜
a
＜
2
3
D．
3
＜
a
＜
4
3
组卷：243引用：3难度：0.7
解析
7．已知矩形ABCD的顶点都在球心为O的球面上，AB=3，
BC
=
3
，且四棱锥O-ABCD的体积为
4
3
，则球O的表面积为（　　）
A．76π B．112π C．
76
3
π
3
D．
224
7
π
3
组卷：287引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，17题10分，其余各题12分，共70分）

21．已知向量
a
=（cos（
π
3
-x），-sinx），
b
=（sin（x+
π
6
），sinx），函数f（x）=
a
•
b
．
（Ⅰ）求函数f（x）的最小正周期和单调递减区间；
（Ⅱ）在△ABC中，角A，B，C的对边分别为a,b,c,若c=2
3
，f（C）=-
1
2
，求△ABC面积的最大值．
组卷：162引用：3难度：0.7
解析
22．如图，在长方体ABCD-A₁B₁C₁D₁中，E，F，G分别为所在棱的中点，H，Q分别为AC，AD₁的中点，连接EF，EG，FG，DQ，CQ，D₁H．
（1）求证：平面EFG∥平面ACQ；
（2）在线段CD上是否存在点P，使得DQ∥平面D₁PH？若存在，求出P点的位置；若不存在，请说出理由．
组卷：551引用：3难度：0.5
解析