当前位置：试卷中心 > 试卷详情

2023-2024学年浙江省嘉兴高级中学高二（上）第一次调研数学试卷

发布：2024/9/26 0:0:1

一、选择题（共8小题，每小题5分，计40分.在每小题给出的四个选项中，只有一个选项正确.）

1．直线x+
3
y+1=0的倾斜角是（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
组卷：1045引用：97难度：0.9
解析
2．已知圆的方程为x²+y²-2x+6y+1=0，那么圆心坐标和半径分别为（　　）
A．（-1，-3），9 B．（1，-3），3 C．（-1，3），3 D．（1，3），9
组卷：343引用：12难度：0.7
解析
3．已知
{
a
，
b
，
c
}
是空间向量的一组基底，
{
a
，
b
+
c
，
b
-
c
}
是空间向量的另一组基底，若向量
p
在基底
{
a
，
b
，
c
}
下的坐标为（2，3，-1），则向量
p
在基底
{
a
，
b
+
c
，
b
-
c
}
下的坐标是（　　）
A．（2，-1，-2） B．（2，-1，2） C．（2，1，-2） D．（2，1，2）
组卷：125引用：4难度：0.7
解析
4．将正方形ABCD沿对角线AC折成直二面角，则异面直线AB与CD夹角的余弦值是（　　）
A．
-
1
2
B．
1
2
C．
3
3
D．
6
3
组卷：29引用：2难度：0.7
解析
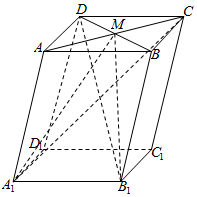5．在平行六面体ABCD-A₁B₁C₁D₁中，M为AC与BD的交点，若
A
1
B
1
=
a
，
A
1
D
1
=
b
，
A
1
A
=
c
，则下列向量运算不正确的是（　　）
A．
B
1
M
=-
1
2
a
+
1
2
b
+
c
B．
B
1
D
=-
a
+
b
+
c
C．
A
1
C
=
a
+
b
+
c
D．
A
1
M
=-
1
2
a
-
1
2
b
+
c
组卷：232引用：3难度：0.7
解析
6．唐代诗人李顾的诗《古从军行》开头两句说“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在区域为x²+y²≤1，若将军从点A（3，0）处出发，河岸线所在直线方程为x+y=4，并假定将军只要到达军营所在区域即回到军营，则“将军饮马”的最短总路程为（　　）
A．
3
2
-
1
B．2 C．
17
D．
17
-
1
组卷：161引用：6难度：0.5
解析
7．已知正方体ABCD-A₁B₁C₁D₁的棱长为2，点E，F分别为棱CD，DD₁的中点，点P为四边形CDD₁C₁内（包括边界）的一动点，且满足B₁P∥平面BEF，则点P的轨迹长为（　　）
A．
2
B．2 C．
2
2
D．1
组卷：48引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共有6个小题，共70分.解答应写出文字说明、证明过程和演算步骤.

21．已知圆E经过点A（0，0），B（1，1），圆E恒被直线mx-y-m=0（m∈R）平分；
（1）求圆E的方程；
（2）过点P（3，0）的直线l与圆E相交于C、D两点，求CD中点M的轨迹方程．
组卷：75引用：3难度：0.5
解析
22．如图1，四边形ABCD是平行四边形，AB=2AD=2，∠ADC=60°，E是CD的中点，将平行四边形ABCD沿着AE翻折，使平面ADE⊥平面ABCE（如图2），点G是△ADE的重心，连结AC，BE交于点F．

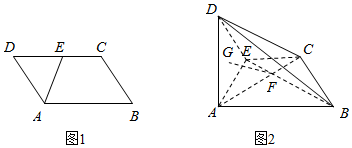
（1）求证：GF∥平面CDE；
（2）求直线GF与平面BCD所成角的正弦值．
组卷：106引用：5难度：0.6
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． B 1 M =- 1 2 a + 1 2 b + c	B． B 1 D =- a + b + c
C． A 1 C = a + b + c	D． A 1 M =- 1 2 a - 1 2 b + c

2023-2024学年浙江省嘉兴高级中学高二（上）第一次调研数学试卷

一、选择题（共8小题，每小题5分，计40分.在每小题给出的四个选项中，只有一个选项正确.）

1．直线x+3y+1=0的倾斜角是（ ）

2．已知圆的方程为x2+y2-2x+6y+1=0，那么圆心坐标和半径分别为（ ）

3．已知{a，b，c}是空间向量的一组基底，{a，b+c，b-c}是空间向量的另一组基底，若向量p在基底{a，b，c}下的坐标为（2，3，-1），则向量p在基底{a，b+c，b-c}下的坐标是（ ）

4．将正方形ABCD沿对角线AC折成直二面角，则异面直线AB与CD夹角的余弦值是（ ）

5．在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若A1B1=a，A1D1=b，A1A=c，则下列向量运算不正确的是（ ）

7．已知正方体ABCD-A1B1C1D1的棱长为2，点E，F分别为棱CD，DD1的中点，点P为四边形CDD1C1内（包括边界）的一动点，且满足B1P∥平面BEF，则点P的轨迹长为（ ）

四、解答题：本题共有6个小题，共70分.解答应写出文字说明、证明过程和演算步骤.

21．已知圆E经过点A（0，0），B（1，1），圆E恒被直线mx-y-m=0（m∈R）平分；（1）求圆E的方程；（2）过点P（3，0）的直线l与圆E相交于C、D两点，求CD中点M的轨迹方程．

1．直线x+
3
y+1=0的倾斜角是（　　）

2．已知圆的方程为x²+y²-2x+6y+1=0，那么圆心坐标和半径分别为（　　）

3．已知
{
a
，
b
，
c
}
是空间向量的一组基底，
{
a
，
b
+
c
，
b
-
c
}
是空间向量的另一组基底，若向量
p
在基底
{
a
，
b
，
c
}
下的坐标为（2，3，-1），则向量
p
在基底
{
a
，
b
+
c
，
b
-
c
}
下的坐标是（　　）

4．将正方形ABCD沿对角线AC折成直二面角，则异面直线AB与CD夹角的余弦值是（　　）

5．在平行六面体ABCD-A₁B₁C₁D₁中，M为AC与BD的交点，若
A
1
B
1
=
a
，
A
1
D
1
=
b
，
A
1
A
=
c
，则下列向量运算不正确的是（　　）

7．已知正方体ABCD-A₁B₁C₁D₁的棱长为2，点E，F分别为棱CD，DD₁的中点，点P为四边形CDD₁C₁内（包括边界）的一动点，且满足B₁P∥平面BEF，则点P的轨迹长为（　　）

21．已知圆E经过点A（0，0），B（1，1），圆E恒被直线mx-y-m=0（m∈R）平分；
（1）求圆E的方程；
（2）过点P（3，0）的直线l与圆E相交于C、D两点，求CD中点M的轨迹方程．