2022-2023学年江西省南昌市青山湖区孺子学校九年级（上）段考数学试卷（12月份）

一、选择题（共6小题，每小题3分，共18分）.

• 1．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（　　）

  A．

  B．

  C．

  D．
  组卷：2247引用：61难度：0.9

  解析

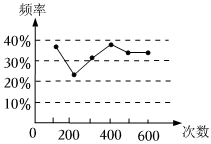• 2．甲、乙两位同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率，绘出的统计图如图所示，则符合这结果的实验可能是（　　）

  A．从一个装有2个白球和1个红球的袋子任取一个球，则取到红球的概率

  B．任意买一张电影票，座位号是偶数的概率

  C．抛一枚质地均匀的硬币，正面朝上的概率

  D．掷一枚正六面体的骰子，出现1点的概率
  组卷：528引用：7难度：0.7

  解析

• 3．已知x₁、x₂是关于x的方程x²-ax-2=0的两根，下列结论一定正确的是（　　）

  A．x1≠x2

  B．x1+x2＞0

  C．x1•x2＞0

  D．x1＜0，x2＜0
  组卷：6271引用：73难度：0.9

  解析

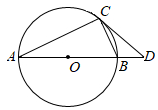• 4．如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，过点C作⊙O的切线，交AB的延长线于点D．设∠A=α，∠D=β，则（　　）

  A．α=β

  B．α+β=90°

  C．2α+β=90°

  D．α+2β=90°
  组卷：510引用：2难度：0.8

  解析

• 5．抛物线y=ax²+bx+c（a＞0）与直线y=bx+c在同一坐标系中的大致图象可能为（　　）

  A．

  B．

  C．

  D．
  组卷：1802引用：16难度：0.6

  解析

• 6．已知二次函数y=ax²+bx+c的自变量x与函数y的部分对应值见表格，则下列结论：①c=2；②b²-4ac＞0；③方程ax²+bx=0的两根为x₁=-2，x₂=0；④7a+c＜0．其中正确的有（　　）
  

  x	…	-3	-2	-1	1	2	…
  y	…	1.875	3	m	1.875	0	…

  A．①④

  B．②③

  C．③④

  D．②④
  组卷：1717引用：9难度：0.4

  解析

二、填空题（共6小题，每小题3分，共18分）

• 7．圆锥的母线长为4cm,底面半径为3cm,那么它的侧面展开图的圆心角是

  度．
  组卷：466引用：6难度：0.7

  解析

五、解答题（共2小题，每小题9分，共18分）

• 22．问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
  【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．
  【类比引申】如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足

  关系时，仍有EF=BE+FD．
  【探究应用】如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（

  3

  -1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：

  2

  =1.41，

  3

  =1.73）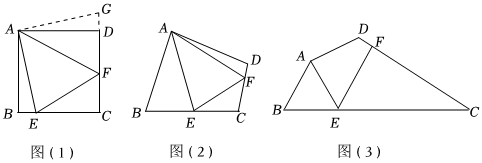
  
  组卷：2549引用：26难度：0.1

  解析

六、（共1小题，每小题12分，共12分）

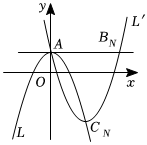• 23．已知抛物线L：y=-x²+1与y轴交于点A．
  （1）点A坐标为

  ；
  （2）如图，点C_n在抛物线L上，其中C_n的横坐标为2ⁿ（n=0，1，2，…），分别记为C₀，C₁，C₂，…，C_n，顶点为C_n的抛物线L'经过点A，交过点A且与x轴平行的直线于点B_n（n=0，1，2，…），分别记为B₀，B₁，B₂，…，B_n．
  ①当n=1时，求经过C₁，B₁两点抛物线L'的解析式；
  ②求B_n，C_n的坐标．（用含n的代数式表示）
  ③求B_nB_n+1及B_nC_n+1的长度．（用含n的代数式表示）
  组卷：16引用：2难度：0.5

  解析