2022-2023学年福建省漳州市立人学校高二（下）第二次月考数学试卷（6月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知向量

  a

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，则向量

  b

  在向量

  a

  上的投影向量为（　　）

  A．（0，-1，-1）

  B．（-1，0，-1）

  C． （ 0 ， 1 2 ， 1 2 ）

  D． （ 1 2 ， 0 ， 1 2 ）
  组卷：215引用：8难度：0.8

  解析

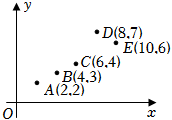• 2．如图，在一组样本数据A（2，2），B（4，3），C（6，4），D（8，7），E（10，6）的散点图中，若去掉D（8，7）后，则下列说法正确的为（　　）

  A．样本相关系数r变小

  B．残差平方和变大

  C．相关指数R2变小

  D．自变量x与因变量y的相关程度变强
  组卷：195引用：2难度：0.8

  解析

• 3．若随机变量X～N（μ，σ²）（σ＞0），则有如下结论：
  （P（|X-μ|＜σ）=0.6826，P（|X-μ|＜2σ）=0.9544，P（|X-μ|＜3σ）=0.9974）
  高三（1）班有40名同学，一次数学考试的成绩服从正态分布，平均分为120，方差为100，理论上说在130分以上人数约为（　　）

  A．19

  B．12

  C．6

  D．5
  组卷：164引用：5难度：0.9

  解析

• 4．现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛，要求每位同学参加一项比赛，每项比赛至少一位同学参加，事件A=“甲参加跳高比赛”，事件B=“乙参加跳高比赛”，事件C=“乙参加跳远比赛”，则（　　）

  A．事件A与B相互独立	B．事件A与C为互斥事件
  C． P （ C | A ） = 5 12	D． P （ B | A ） = 1 9
  组卷：546引用：22难度：0.5

  解析

• 5．已知函数

  f

  （

  x

  ）

  =

  x

  2

  +

  1

  4

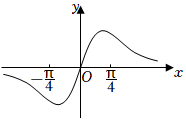  ，g（x）=sinx,则图象为如图的函数可能是（　　）

  A．y=f（x）g（x）	B． y = g （ x ） f （ x ）
  C． y = f （ x ） + g （ x ） - 1 4	D． y = f （ x ） - g （ x ） - 1 4
  组卷：294引用：12难度：0.7

  解析

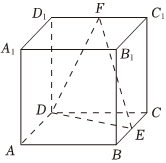• 6．如图，在正方体ABCD-A₁B₁C₁D₁中，棱长为2，点E，F分别为棱BC、C₁D₁中点，则点A₁到平面DEF的距离为（　　）

  A．2

  B． 10 21 21

  C． 7 23 23

  D． 21 7
  组卷：105引用：2难度：0.5

  解析

• 7．已知函数f（x）在R上满足f（1+x）=2f（1-x）-x²+3x+1，则曲线y=f（x）在点（1，f（1））处的切线方程是（　　）

  A．3x-y-2=0

  B．3x+y-2=0

  C．x-y+1=0

  D．x-y-2=0
  组卷：51引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．某车间购置了三台机器，这种机器每年需要一定次数的维修，现统计了100台这种机器一年内维修的次数，其中每年维修2次的有40台，每年维修3次的有60台，用X代表这三台机器每年共需要维修的次数．
  （1）以频率估计概率，求X的分布列与数学期望；
  （2）维修厂家有A，B两家，假设每次仅维修一台机器，其中A厂家单次维修费用是550元，B厂家对同一车间的维修情况进行记录，前5次维修费用是每次600元，后续维修费用每次递减100元，从每年的维修费用的期望角度来看，选择哪家厂家维修更加节省？
  组卷：57引用：3难度：0.5

  解析

• 22．已知函数f（x）=sinx-ln（1+x），f′（x）为f（x）的导数．证明：
  （1）f′（x）在区间（-1，

  π

  2

  ）存在唯一极大值点；
  （2）f（x）有且仅有2个零点．
  组卷：11689引用：12难度：0.2

  解析