2022-2023学年重庆市巴蜀中学高三（下）月考数学试卷（4月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合N={x|e^x＞1}，若集合M满足N∩M=M，则M可能是（　　）

  A．{0，1，2，3}

  B．{x|x2=9}

  C．{x|x≥3}

  D．R
  组卷：41引用：4难度：0.7

  解析

• 2．命题：“∀x∈[1，2]，2x²-3≥0”的否定是（　　）

  A．∀x∉[1，2]，2x2-3≥0	B．∀x∈[1，2]，2x2-3＜0
  C．∃x0∈[1，2]，2 x 2 0 -3＜0	D．∃x0∉[1，2]，2 x 2 0 -3＜0
  组卷：203引用：6难度：0.9

  解析

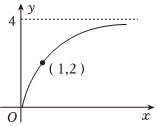• 3．已知函数f（x）的部分图象如图所示，则它的一个可能的解析式为（　　）

  A． y = 2 x

  B． y = 4 - 4 x + 1

  C．y=3x-5

  D． y = 3 x
  组卷：30引用：2难度：0.8

  解析

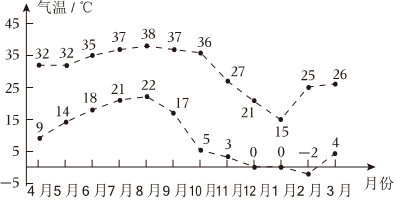• 4．如图是遂宁市2022年4月至2023年3月每月最低气温与最高气温（℃）的折线统计图：已知每月最低气温与最高气温的线性相关系数r=0.88，则下列结论正确的是（　　）

  A．月温差（月最高气温-月最低气温）的最大值出现在8月

  B．每月最低气温与最高气温有较强的线性相关性，且二者为线性负相关

  C．每月最高气温与最低气温的平均值在4-8月逐月增加

  D．9-12月的月温差相对于5-8月，波动性更小
  组卷：64引用：6难度：0.7

  解析

• 5．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左，右焦点分别为F₁，F₂，O为坐标原点，过F₁作C的一条渐近线的垂线，垂足为D，且|DF₂|=2

  2

  |OD|，则C的离心率为（　　）

  A． 2

  B．2

  C． 5

  D．3
  组卷：620引用：11难度：0.5

  解析

• 6．已知a,b,c均为负实数，且

  a

  =

  ln

  a

  +

  1

  3

  +

  2

  ，

  b

  =

  ln

  b

  +

  1

  4

  +

  3

  ，c=2e^c-1-1，则（　　）

  A．b＜a＜c

  B．c＜b＜a

  C．a＜b＜c

  D．a＜c＜b
  组卷：245引用：9难度：0.6

  解析

• 7．已知正四棱锥O-ABCD的底面边长为

  6

  ，高为3．以点O为球心，

  2

  为半径的球O与过点A，B，C，D的球O₁相交，相交圆的面积为π，则球O₁的半径为（　　）

  A． 13 2 或 6

  B． 13 2 或 97 4

  C． 3 或 97 4

  D． 3 或 6
  组卷：209引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆

  C

  ：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的上、下顶点分别为A₁，A₂，点

  P

  （

  2

  2

  ，

  1

  ）

  在C上，且

  P

  A

  1

  •

  P

  A

  2

  =

  -

  1

  2

  ．
  （1）求椭圆C的标准方程；
  （2）设坐标原点为O，若不经过点P的直线与C相交于M，N两点，直线PM与PN的斜率互为相反数，当△MON的面积最大时，求直线MN的方程．
  组卷：65引用：3难度：0.5

  解析

• 22．帕德近似是法国数学家亨利•帕德发明的用有理多项式近似特定函数的方法．给定两个正整数m,n,函数f（x）在x=0处的[m,n]阶帕德近似定义为：

  R

  （

  x

  ）

  =

  a

  0

  +

  a

  1

  x

  +

  ⋯

  +

  a

  m

  x

  m

  1

  +

  b

  1

  x

  +

  ⋯

  +

  b

  n

  x

  n

  ，且满足：f（0）=R（0），f'（0）=R'（0），f″（0）=R″（0）…，f^（m+n）（0）=R^（m+n）（0）．已知f（x）=ln（x+1）在x=0处的[1，1]阶帕德近似为

  R

  （

  x

  ）

  =

  ax

  1

  +

  bx

  ．
  注：f″（x）=[f'（x）]′，f″'（x）=[f″（x）]′，f^（4）（x）=[f″'（x）]′，f^（5）（x）=[f^（4）（x）]′，…
  （1）求实数a,b的值；
  （2）求证：

  （

  x

  +

  b

  ）

  f

  （

  1

  x

  ）

  ＞

  1

  ；
  （3）求不等式

  （

  1

  +

  1

  x

  ）

  x

  ＜

  e

  ＜

  （

  1

  +

  1

  x

  ）

  x

  +

  1

  2

  的解集，其中e=2.71828⋯．
  组卷：216引用：9难度：0.2

  解析