2023-2024学年湖南省常德市临澧一中高三(上)第二次段考数学试卷
发布:2024/9/1 0:0:9
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1.已知集合A={x|lnx<1},B={x|-1<x<2},则A∩B=( )
组卷:125引用:11难度:0.9 -
2.设i为虚数单位,复数z满足iz+1=(1-i)2,则|1+z|=( )
组卷:143引用:3难度:0.8 -
3.若向量
,a满足b,|a|=1,|b|=2,则a⊥(a+b)与a的夹角为( )b组卷:840引用:19难度:0.7 -
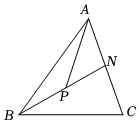 4.如图,在△ABC中,,P是BN的中点,若AN=12AC,则m+n=( )AP=mAB+nAC组卷:1527引用:11难度:0.8
4.如图,在△ABC中,,P是BN的中点,若AN=12AC,则m+n=( )AP=mAB+nAC组卷:1527引用:11难度:0.8 -
5.若cos(
-α)=π4,则sin2α=( )35组卷:12553引用:109难度:0.7 -
6.已知数列
为等比数列,且a3=1,a7=21,则a9=( ){ann}组卷:237引用:4难度:0.8 -
7.已知
,x1=ln12,x3满足x2=223,则( )ex3=log12x3组卷:62引用:3难度:0.7
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤.))
-
21.记锐角△ABC的内角A,B,C的对边分别为a,b,c,已知
.sin(A-B)cosB=sin(A-C)cosC
(1)求证:B=C;
(2)若asinC=1,求的最大值.1a2+1b2组卷:611引用:9难度:0.5 -
22.已知数列{an}为等差数列,数列{bn}为等比数列,且a4=7,a1=1,a1+b3=
,a2b3=4a3+b2(n∈N+).a22
(1)求{an},{bn}的通项公式;
(2)已知cn=,求数列{cn}的前2n项和T2n;anbn,n为奇数,(3an-4)bnanan+2,n为偶数.
(3)求证:.n∑i=11ai+1log2bi<23组卷:130引用:4难度:0.5


