当前位置：试卷中心 > 试卷详情

2022-2023学年河南省周口恒大中学高一（下）月考数学试卷（5月份）

发布：2024/5/17 8:0:8

1．若a=2^0.5，b=log₃2，c=log₂0.2，则（　　）
A．a＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a
组卷：122引用：3难度：0.8
解析
2．已知函数
f
（
x
）
=
sin
（
ωx
-
π
3
）
（
ω
＞
0
）
，x∈[0，π]的值域为
[
-
3
2
，
1
]
，则ω的取值范围是（　　）
A．
[
1
3
，
5
3
]
B．
[
5
6
，
1
]
C．
[
5
6
，
5
3
]
D．（0，+∞）
组卷：296引用：11难度：0.8
解析
3．
co
s
2
π
12
-
co
s
2
5
π
12
等于（　　）
A．
1
2
B．
3
3
C．
2
2
D．
3
2
组卷：282引用：10难度：0.8
解析
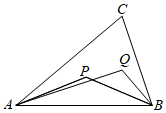4．如图，设P、Q为△ABC内的两点，且
AP
=
2
5
AB
+
1
5
AC
，
AQ
=
2
3
AB
+
1
4
AC
，则△ABP的面积与△ABQ的面积之比为（　　）
A．
1
5
B．
4
5
C．
1
4
D．
1
3
组卷：417引用：22难度：0.9
解析
5．若（x+3i）²是纯虚数（其中i为虚数单位），则实数x=（　　）
A．3 B．±1 C．-1 D．±3
组卷：6引用：3难度：0.8
解析
6．设函数
f
（
x
）
=
（
x
+
1
）
2
，
x
＜
1
4
-
x
-
1
，
x
≥
1
则使得f（-1）+f（m-1）=1成立的m的值为（　　）
A．10 B．0，-2 C．0，-2，10 D．1，-1，11
组卷：28引用：2难度：0.9
解析
7．下列关系正确的是（　　）
A．
2
∈
N
B．-1∈N C．
1
2
∈
N
D．0∈N
组卷：851引用：1难度：0.9
解析

21．设函数f_k（x）=2^x+（k-1）•2^-x（x∈R，k∈Z）．
（1）若f_k（x）是偶函数，求实数k的值；
（2）若存在x∈[1，2]，使得f₀（x）+mf₁（x）≤4成立，求实数m的取值范围．
组卷：73引用：2难度：0.3
解析
22．定义在非零实数集上的函数f（x）对任意非零实数x,y都满足
f
（
x
y
）
+
2
f
（
y
x
）
=
2
x
-
y
x
．
（1）求f（2）的值；
（2）求f（x）的解析式；
（3）设函数g（x）=xf（x），求g（x）在区间
[
1
4
，
2
m
]
上的最大值h（m）．
组卷：75引用：2难度：0.5
解析

1．若a=20.5，b=log32，c=log20.2，则（ ）