2022-2023学年广东省佛山四中八年级（上）期中数学试卷

一、单选题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一项是正确的，请把答题卡上对应题目所选的选项涂黑。

• 1．下列实数是无理数的是（　　）

  A． 1 3	B．0.1010010001
  C．π	D． 9
  组卷：271引用：6难度：0.8

  解析

• 2．能作为直角三角形的三边长的数据是（　　）

  A．3，4，6

  B．5，12，14

  C．1， 3 ，2

  D． 2 ， 3 ，2
  组卷：516引用：4难度：0.7

  解析

• 3．在平面直角坐标系中，点A的坐标为（-2，3），则点A关于y轴对称点的坐标是（　　）

  A．（-2，-3）

  B．（-2，3）

  C．（2，-3）

  D．（2，3）
  组卷：249引用：4难度：0.8

  解析

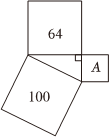• 4．若三个正方形的面积如图所示，则正方形A的面积为（　　）

  A．6

  B．36

  C．64

  D．8
  组卷：625引用：14难度：0.9

  解析

• 5．如果点P（m+3，m+1）在直角坐标系的x轴上，那么P点坐标为（　　）

  A．（0，2）

  B．（2，0）

  C．（4，0）

  D．（0，-4）
  组卷：995引用：22难度：0.7

  解析

• 6．下列等式正确的是（　　）

  A． （ - 7 ） 2 =-7

  B． 81 =±9

  C．- 3 - 8 27 = 2 3

  D． - 9 =-3
  组卷：338引用：5难度：0.7

  解析

• 7．若b＞0，则一次函数y=-x+b的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：3835引用：24难度：0.7

  解析

三、解答题（本大题8小题，18～20题每小题6分，21～23题每小题6分，24～25题每小题6分，共62分）

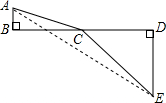• 22．为了探索代数式

  x

  2

  +

  1

  +

  （

  8

  -

  x

  ）

  2

  +

  25

  的最小值，
  小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=1，DE=5，BD=8，设BC=x.则AC=

  x

  2

  +

  1

  ，CE=

  （

  8

  -

  x

  ）

  2

  +

  25

  则问题即转化成求AC+CE的最小值．
  （1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得

  x

  2

  +

  1

  +

  （

  8

  -

  x

  ）

  2

  +

  25

  的最小值等于

  ，此时x=

  ；
  （2）题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想？
  （选填：函数思想，分类讨论思想、类比思想、数形结合思想）
  （3）请你根据上述的方法和结论，试构图求出代数式

  x

  2

  +

  4

  +

  （

  12

  -

  x

  ）

  2

  +

  9

  的最小值

  ．
  组卷：649引用：4难度：0.5

  解析

• 23．在如图的正方形网格中，每一个小正方形的边长为1，格点三角形ABC（顶点是网格线交点的三角形）的三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
  （1）请在图中的网格平面内建立平面直角坐标系，并将△ABC画出来．
  （2）在图中找一点D，使AD=

  26

  ，CD=

  13

  ，并将点D标记出来．
  （3）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标．
  （4）在y轴上是否存在点Q，使得S_△AOQ=

  1

  2

  S_△ABC，如果存在，求出点Q的坐标，如果不存在，说明理由．
  组卷：64引用：2难度：0.5

  解析