为了探索代数式x2+1+（8-x）2+25的最小值，
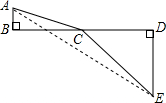
小张巧妙的运用了数学思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=1，DE=5，BD=8，设BC=x.则AC=x2+1，CE=（8-x）2+25则问题即转化成求AC+CE的最小值．
（1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得x2+1+（8-x）2+25的最小值等于 1010，此时x=4343；
（2）题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想？
（选填：函数思想，分类讨论思想、类比思想、数形结合思想）
（3）请你根据上述的方法和结论，试构图求出代数式x2+4+（12-x）2+9的最小值 1313．
x
2
+
1
+
（
8
-
x
）
2
+
25
x
2
+
1
（
8
-
x
）
2
+
25
x
2
+
1
+
（
8
-
x
）
2
+
25
4
3
4
3
x
2
+
4
+
（
12
-
x
）
2
+
9
【考点】轴对称-最短路线问题．
【答案】10；；13
4
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 19:0:1组卷：652引用：4难度：0.5
相似题
-
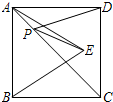1．如图，正方形ABCD的边长是2，以正方形ABCD的边AB为边，在正方形内作等边三角形ABE，P为对角线AC上的一点，则PD+PE的最小值为．发布：2025/6/18 21:0:1组卷：396引用：40难度：0.7 -
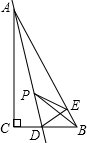2．如图，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是．发布：2025/6/18 21:0:1组卷：2636引用：69难度：0.7 -
3．已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值=．发布：2025/6/18 21:0:1组卷：2780引用：91难度：0.5
