2022-2023学年重庆市涪陵区八年级（上）期末数学试卷

一、选择题。（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

• 1．下列图形分别是安全饮品、国家节水、绿色食品、循环再生的环保标志，其中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：74引用：4难度：0.9

  解析

• 2．若分式

  1

  x

  -

  5

  有意义，则x的取值范围是（　　）

  A．x≠5

  B．x=5

  C．x＜5

  D．x＞5
  组卷：212引用：6难度：0.8

  解析

• 3．已知一个三角形的两边长分别为5cm、9cm,则这个三角形的第三边长可能是（　　）

  A．3cm

  B．4cm

  C．6cm

  D．15cm
  组卷：94引用：1难度：0.6

  解析

• 4．下列计算正确的是（　　）

  A．a3•a2=a6

  B．a8÷a2=a6

  C．（2a2）3=6a6

  D．4a3-2a3=2
  组卷：137引用：1难度：0.8

  解析

• 5．一个多边形的内角和是900°，则这个多边形的边数是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：1888引用：26难度：0.7

  解析

• 6．如图，已知AB=AD，下列条件中，添加后仍不能判定△ABC≌△ADC的是（　　）

  A．∠ACB=∠ACD

  B．∠BAC=∠DAC

  C．∠B=∠D=90°

  D．BC=DC
  组卷：154引用：2难度：0.6

  解析

• 7．若（x-1）（x+m）=x²+2x-3，则常数m的值为（　　）

  A．3

  B．2

  C．-3

  D．-2
  组卷：949引用：1难度：0.6

  解析

• 8．下列因式分解正确的是（　　）

  A．a2+a=a（a+1）	B．m2-4=（m+4）（m-4）
  C．2x2+4x-2=2（x2+2x）	D．a2-2a+1=a（a-2）+1
  组卷：466引用：6难度：0.7

  解析

四、解答题。（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

• 24．对于一个三位数M，如果它的百位数字与它的十位数字之和为10，则称M是“十成九稳数”．
  例如：287，∵2+8=10，∴287是“十成九稳数”．
  又如：454，∵4+5=9≠10，∴454不是“十成九稳数”．
  （1）判断375，602是否是“十成九稳数”？说明理由；
  （2）已知一个“十成九稳数”N=100a+10b+c（其中1≤a≤9，0≤b≤9，0≤c≤9，且a,b,c都是整数），把百位数字的3倍记作F（N），百位数字与十位数字的和减去个位数字的差记作T（N），若F（N）•T（N）=36，求满足条件的所有N．
  组卷：103引用：2难度：0.6

  解析

• 25．如图，在Rt△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点，连结CD，过点B作BE⊥CD交CD的延长线于点E．
  
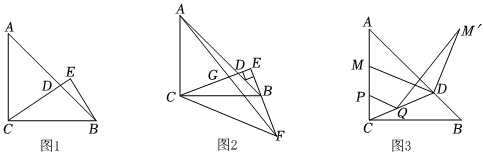
  （1）如图1，若∠BCE=2∠DBE，BE=4，求△ABC的面积；
  （2）如图2，延长EB到点F使EF=CE，分别连结CF，AF，AF交EC于点G．求证：BF=2EG；
  （3）如图3，若AC=AD，点M是直线AC上的一个动点，连结MD，将线段MD绕点D顺时针方向旋转90°得到线段M'D，点P是AC边上一点，AP=3PC，Q是线段CD上的一个动点，连结PQ，QM'．当PQ+QM'的值最小时，请直接写出∠PQM'的度数．
  组卷：613引用：3难度：0.3

  解析