对于一个三位数M，如果它的百位数字与它的十位数字之和为10，则称M是“十成九稳数”．
例如：287，∵2+8=10，∴287是“十成九稳数”．
又如：454，∵4+5=9≠10，∴454不是“十成九稳数”．
（1）判断375，602是否是“十成九稳数”？说明理由；
（2）已知一个“十成九稳数”N=100a+10b+c（其中1≤a≤9，0≤b≤9，0≤c≤9，且a,b,c都是整数），把百位数字的3倍记作F（N），百位数字与十位数字的和减去个位数字的差记作T（N），若F（N）•T（N）=36，求满足条件的所有N．
【考点】整式的加减．
【答案】（1）375是“十成九稳数”，602不是“十成九稳数”；
（2）284，376，467，648．
（2）284，376，467，648．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：103引用：2难度：0.6
相似题
-
1．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
×2x=4x2-6xy+2x,则所指的多项式为 ．发布：2025/6/7 22:0:1组卷：287引用：8难度：0.7 -
2．先阅读下列材料，然后解后面的问题．
材料：一个三位自然数（百位数字为a,十位数字为b,个位数字为c），若满足a+c=b,则称这个三位数为“欢喜数”，并规定F（abc）=ac,如275，因为它的百位上数字2与个位数字5之和等于十位上的数字7，所以275是“欢喜数”，∴F（275）=2×5=10．abc
（1）求证：任意一个“欢喜数”都能被11整除；abc
（2）已知有两个十位数字相同的“欢喜数”m,n（m＞n），若F（m）-F（n）=3，求m-n的值．发布：2025/6/7 19:30:2组卷：28引用：3难度：0.7 -
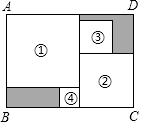3．将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示．设右上角与左下角阴影部分的周长的差为l.若知道l的值，则不需测量就能知道周长的正方形的标号为（ ）发布：2025/6/7 17:30:1组卷：3268引用：17难度：0.7
