2022-2023学年江苏省扬州大学附中高二（下）期中数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项符合要求)

• 1．下列求导运算正确的是（　　）

  A．（sinx）'=-cosx	B． （ 1 x ） ′ = lnx
  C．（ax）'=xax-1	D． （ x ） ′ = 1 2 x
  组卷：523引用：10难度：0.7

  解析

• 2．2023×2022×2021×2020×…×1984×1983等于（　　）

  A． C 40 2023

  B． C 41 2023

  C． A 40 2023

  D． A 41 2023
  组卷：115引用：1难度：0.8

  解析

• 3．（x+

  1

  x

  ）⁸展开式中的常数项为（　　）

  A．70

  B．56

  C．28

  D．-70
  组卷：57引用：1难度：0.8

  解析

• 4．有4名新冠疫情防控志愿者，每人从3个不同的社区中选择1个进行服务．则不同的选择办法共有（　　）

  A．81种

  B．72种

  C．64种

  D．48种
  组卷：27引用：2难度：0.8

  解析

• 5．平面α的一个法向量是

  n

  =（

  1

  2

  ，-1，

  1

  3

  ），平面β的一个法向量是

  m

  =（-3，6，-2），则平面α与平面β的关系是（　　）

  A．平行

  B．重合

  C．平行或重合

  D．垂直
  组卷：118引用：8难度：0.8

  解析

• 6．如图，空间四边形的各边和对角线长均相等，E是BC的中点，那么（　　）

  A． AE • BC ＜ AE • CD

  B． AE • BC = AE • CD

  C． AE • BC ＞ AE • CD

  D． AE • BC 与  AE • CD 不能比较大小
  组卷：39引用：2难度：0.7

  解析

• 7．如图，在直三棱柱ABC-A₁B₁C₁中，∠BCA=90°，AC=CC₁=2，M是A₁B₁的中点，以C为坐标原点，建立如图所示的空间直角坐标系．若

  A

  1

  B

  ⊥

  C

  1

  M

  ，则异面直线CM与A₁B所成角的余弦值为（　　）

  A． 2 3

  B． 3 3

  C． 2 3

  D． 7 3
  组卷：138引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共70分解答应写出必要的文字说明、证明过程或演算步骤）

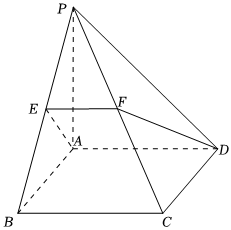• 21．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧面PAD为等腰直角三角形，且

  ∠

  PAD

  =

  π

  2

  ，点F为棱PC上的点，平面ADF与棱PB交于点E．
  （Ⅰ）求证：EF∥AD；
  （Ⅱ）从条件①、条件②、条件③这三个条件中选择两个作为已知，求平面PCD与平面ADFE所成锐二面角的大小．
  条件①：

  AE

  =

  2

  ；
  条件②：平面PAD⊥平面ABCD；
  条件③：PB⊥FD．
  注：如果选择的条件不符合要求，第（Ⅱ）问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．
  组卷：681引用：9难度：0.4

  解析

• 22．已知函数f（x）=e^x-ax²（e是自然对数的底数，a∈R）．
  （1）设f（x）的导函数为f′（x），试讨论f'′（x）的单调性；
  （2）当a=e时，若x₀是f（x）的极大值点，判断并证明f（x₀）与

  3

  e

  4

  大小关系．
  组卷：247引用：3难度：0.1

  解析