2022-2023学年四川省达州市渠县二中八年级（上）月考数学试卷

一、选择题（共32分）

• 1．下列实数中，是无理数的是（　　）

  A．0.10010001

  B． 4

  C． 22 7

  D． 3
  组卷：6引用：1难度：0.5

  解析

• 2．式子

  x

  +

  2

  在实数范围内有意义，则x的取值范围是（　　）

  A．x＞-2

  B．x≥-2

  C．x≠-2

  D．x≤-2
  组卷：111引用：6难度：0.8

  解析

• 3．下面各组数中，是勾股数的是（　　）

  A．9，16，25	B．0.3，0.4，0.5
  C．1，3，2	D．7，24，25
  组卷：332引用：8难度：0.6

  解析

• 4．下列计算正确的是（　　）

  A． 3 + 2 3 = 5 3

  B． 3 ÷ 5 = 15 5

  C． 5 3 × 2 3 = 10 3

  D． 4 3 - 3 3 = 1
  组卷：201引用：2难度：0.7

  解析

• 5．满足下列条件的△ABC，不是直角三角形的是（　　）

  A．a：b：c=3：4：5	B．∠A：∠B：∠C=9：12：15
  C．∠C=∠A-∠B	D．b2-a2=c2
  组卷：644引用：8难度：0.9

  解析

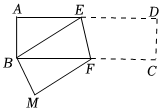• 6．已知，如图长方形ABCD中，AB=3cm,AD=9cm,将此长方形折叠，使点D与点B重合，折痕为EF，则BE的长为（　　）

  A．6cm

  B．9cm

  C．4cm

  D．5cm
  组卷：40引用：1难度：0.9

  解析

• 7．下列说法：
  ①

  81

  的算术平方根是9；
  ②无理数是无限小数；
  ③一个直角三角形的两边长分别为3和4，则第三边长为5；
  ④

  π

  3

  是分数；
  ⑤

  5

  既是二次根式，又是整式；
  ⑥实数和数轴上的点是一一对应的．
  其中正确的有（　　）个．

  A．1

  B．2

  C．3

  D．4
  组卷：44引用：1难度：0.6

  解析

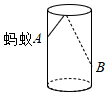• 8．如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm,底面周长为16cm,在容器内壁离容器底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（　　）

  A．20cm

  B．4 13 cm

  C．10cm

  D．2 73 cm
  组卷：1040引用：7难度：0.5

  解析

五、解答题（本大题共3个小题，共30分）

• 25．阅读材料：学习了无理数后，某数学兴趣小组开展了一次探究活动：估算

  13

  的近似值．
  小明的方法：
  ∵

  9

  ＜

  13

  ＜

  16

  ，设

  13

  =3+k（0＜k＜1），
  ∴（

  13

  ）²=（3+k）².∴13=9+6k+k²．
  ∴13≈9+6k,解得k≈

  2

  3

  ．∴

  13

  ≈3+

  2

  3

  ≈3.67．
  （上述方法中使用了完全平方公式：（a+b）²=a²+2ab+b²，下面可参考使用）问题：
  （1）请你依照小明的方法，估算

  41

  的值（结果保留两位小数）；
  （2）请结合上述具体实例，概括出估算

  m

  的公式：已知非负整数a、b、m,若a＜

  m

  ＜a+1，且m=a²+b,估计

  m

  的值（用含a、b的代数式表示）；
  （3）请用（2）中的结论估算

  37

  的近似值．
  组卷：53引用：1难度：0.5

  解析

• 26．阅读下面材料，并解决问题：
  （1）如图（1），等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，则∠APB=

  .由于PA，PB，PC不在同一个三角形中，为了解决本题，我们可以将△ABP绕顶点A逆时针旋转60°，得到△ACD，此时△ACD≌

  .这样就可以利用全等三角形知识，将三条线段长度转化到一个三角形中，从而求出∠APB的度数．请给出计算证明过程．
  （2）请你利用（1）题的解答思想和方法，解答下面的问题：已知：如图（2），△ABC中，∠CAB=90°，AB=AC，D，E为BC上的点且∠DAE=45°，请你探索线段BD，DE，EC三条线段之间的数量关系，并证明你的结论．
  （3）请你利用第（2）题的结论，解答下面的问题已知：如图（3）△ABC中，∠BAC=90°，AB=AC，D，E为BC上的点，∠DAE=45°，BD=3，CE=4，求DE的长．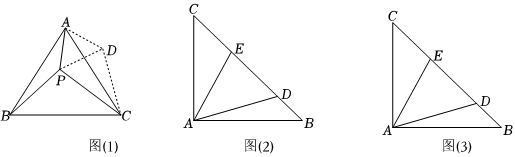
  组卷：98引用：1难度：0.3

  解析