2022-2023学年江苏省徐州市高一（下）期中数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知i为虚数单位，则i²⁰³³=（　　）

  A．i

  B．-i

  C．1

  D．-1
  组卷：16引用：2难度：0.8

  解析

• 2．△ABC的三个内角A，B，C所对边的长分别为a,b,c,设向量

  p

  =

  （

  a

  +

  c

  ,

  b

  ）

  ，

  q

  =

  （

  b

  +

  a

  ,

  c

  -

  a

  ）

  ．若

  p

  ∥

  q

  ，则角C的大小为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． π 2
  组卷：251引用：6难度：0.8

  解析

• 3．复数z满足z（1+i）=|1-

  3

  i|，则复数z=（　　）

  A． 2 （cos π 4 +isin π 4 ）	B． 2 （cos 3 π 4 +isin 3 π 4 ）
  C． 2 （cos π 4 -isin π 4 ）	D． 2 （cos 7 π 4 -isin 7 π 4 ）
  组卷：55引用：4难度：0.7

  解析

• 4．定义：

  |

  a

  ×

  b

  |

  =

  |

  a

  |

  |

  b

  |

  sinθ

  ，其中θ为向量

  a

  ，

  b

  的夹角，若

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  5

  ，

  （

  a

  +

  b

  ）

  •

  a

  =

  -

  2

  ，则

  |

  a

  ×

  b

  |

  =（　　）

  A．6

  B．-6

  C．-8

  D．8
  组卷：28引用：2难度：0.8

  解析

• 5．等腰三角形底和腰之比为黄金分割比的三角形称为黄金三角形，它是最美的三角形．例如，正五角星由5个黄金三角形和一个正五边形组成，且每个黄金三角形都是顶角为36°的等腰三角形，如图所示，在黄金三角形ABC中，

  BC

  AC

  =

  5

  -

  1

  2

  ．根据这些信息，可求得cos144°的值为（　　）

  A． 1 - 5 4

  B． - 5 - 1 2

  C． - 5 + 1 4

  D． - 3 + 5 8
  组卷：98引用：2难度：0.7

  解析

• 6．已知cosα=

  5

  5

  ，sin（β-α）=

  -

  10

  10

  ，α，β均为锐角，则β=（　　）

  A． π 4

  B． π 8

  C． π 3

  D． π 6
  组卷：393引用：6难度：0.7

  解析

• 7．已知点P是△ABC所在平面内一点，有下列四个等式：
  甲：

  PA

  +

  PB

  +

  PC

  =

  0

  ；乙：

  PA

  •

  （

  PA

  -

  PB

  ）

  =

  PC

  •

  （

  PA

  -

  PB

  ）

  ；
  丙：|

  PA

  |=|

  PB

  |=|

  PC

  |；丁：

  PA

  •

  PB

  =

  PB

  •

  PC

  =

  PC

  •

  PA

  ．
  如果只有一个等式不成立，则该等式为（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：602引用：11难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤.

• 21．已知函数为f（x）=asinx+bcosx,称向量

  p

  =（a,b）为f（x）的特征向量，f（x）为

  p

  的特征函数．
  （1）若

  g

  （

  x

  ）

  =

  sin

  （

  x

  +

  π

  3

  ）

  +

  cos

  （

  x

  -

  π

  6

  ）

  ，求g（x）的特征向量；
  （2）设向量

  p

  =

  （

  3

  ，-

  1

  ）

  ，

  q

  =

  （

  1

  ，

  3

  ）

  的特征函数分别为p（x），q（x）．记函数h（x）=p（x）q（x）．
  （i）求h（x）的单调增区间；
  （ii）若方程

  h

  （

  x

  ）

  =

  2

  3

  在（0，π）上的解为x₁，x₂，求cos（x₁-x₂）．
  组卷：39引用：2难度：0.5

  解析

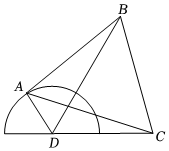• 22．为提升城市旅游景观面貌，城建部门拟对一公园进行改造，已知原公园是直径为200米的半圆，出入口在圆心D处，C点为一居民小区，CD距离为200米，按照设计要求，取圆弧上一点A，并以线段AC为一边向圆外作等边三角形ABC，使改造之后的公园成四边形ABCD，并将△BCD区域建成免费开放的植物园，如图所示．
  （1）若DA⊥DC时，点B与出入口D的距离为多少米？
  （2）A设计在什么位置时，免费开放的植物园区域△BCD面积最大？并求此最大面积．
  组卷：105引用：3难度：0.4

  解析