当前位置：试卷中心 > 试卷详情

2022-2023学年陕西省西安三中高二（下）第二次测评数学试卷（理科）

发布：2024/6/29 8:0:10

一、选择题（本题共12小题，每小题5分，共60分）

1．已知集合A={y|y=2^x-1}，B={x|y=log_0.5（2-x）}，则A∩B=（　　）
A．（-1，2] B．（-1，2） C．（-∞，2] D．（-∞，2）
组卷：160引用：3难度：0.7
解析
2．设x∈R，向量
a
=
（
1
，
2
）
，
b
=
（
x
,
1
）
，
c
=
（
4
，
x
）
．则“
a
⊥
b
”是“
b
∥
c
”的（　　）
A．充分不必要文件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：138引用：6难度：0.7
解析
3．已知命题p：∀x≥0，x²-x≥0，则￢p为（　　）
A．∃x＜0，x²-x＜0 B．∀x＜0，x²-x＜0
C．∃x≥0，x²-x＜0 D．∀x≥0，x²-x＜0
组卷：103引用：3难度：0.8
解析
4．随机变量X的分布列如下，则D（X）的最大值是（　　）

X 0 1

P a b

A．
1
4
B．
1
3
C．
1
2
D．
2
3
组卷：31引用：1难度：0.5
解析
5．设命题p：方程
x
2
k
+
1
+
y
2
3
-
k
=
1
表示焦点在y轴上的椭圆；命题q：方程
x
2
k
+
1
+
y
2
k
-
2
=
1
表示焦点在x轴上的双曲线，若p∧q为真，则实数k的取值范围（　　）
A．-1＜k＜1 B．-1＜k＜2 C．1＜k＜3 D．2＜k＜3
组卷：16引用：5难度：0.8
解析
6．某射手每次射击击中目标的概率均为P（0＜P＜1），且各次射击的结果互不影响．设随机变量X为该射手在n次射击中击中目标的次数，若
E
（
X
）
=
4
，
D
（
X
）
=
4
3
，则P的值为（　　）
A．
1
4
B．
1
3
C．
2
3
D．
3
4
组卷：52引用：3难度：0.7
解析
7．已知a=
2
π
∫
2
0
4
-
x
2
dx,若（1-ax）²⁰¹⁸=b₀+b₁x+b₂x²+…+b₂₀₁₈x²⁰¹⁸（x∈R），则
b
1
2
+
b
2
2
2
+
…
+
b
2018
2
2018
的值为（　　）
A．0 B．-1 C．1 D．2
组卷：138引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共6小题，共70分）

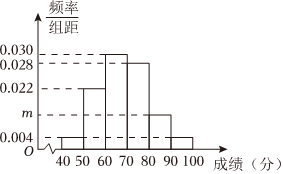21．地区期末进行了统一考试，为做好本次考试的评价工作，将本次成绩转化为百分制，现从中随机抽取了50名学生的成绩，经统计，这批学生的成绩全部介于40至100之间，将数据按照[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分成6组，制成了如图所示的频率分布直方图．
（1）求频率分布直方图中m的值；
（2）在这50名学生中用分层抽样的方法从成绩在[70，80），[80，90），[90，100]的三组中抽取了11人，再从这11人中随机抽取3人，记ξ为3人中成绩在[80，90）的人数，求ξ的分布列和数学期望；
（3）转化为百分制后，规定成绩在[90，100]的为A等级，成绩在[70，90）的为B等级，其它为C等级．以样本估计总体，用频率代替概率．从所有参加考试的同学中随机抽取3人，求获得B等级的人数不少于2人的概率．
组卷：243引用：4难度：0.6
解析
22．在某公司举行的一次真假游戏的有奖竞猜中，设置了“科技”和“生活”这两类试题，规定每位职工最多竞猜3次，每次竞猜的结果相互独立．猜中一道“科技”类试题得4分，猜中一道“生活”类试题得2分，两类试题猜不中的都得0分．将职工得分逐次累加并用X表示，如果X的值不低于4分就认为通过游戏的竞猜，立即停止竞猜，否则继续竞猜，直到竞猜完3次为止．竞猜的方案有以下两种：方案1：先猜一道“科技”类试题，然后再连猜两道“生活”类试题；
方案2：连猜三道“生活”类试题．
设职工甲猜中一道“科技”类试题的概率为0.5，猜中一道“生活”类试题的概率为0.6．
（1）你认为职工甲选择哪种方案通过竞猜的可能性大？并说明理由．
（2）职工甲选择哪一种方案所得平均分高？并说明理由．
组卷：153引用：3难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．充分不必要文件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

A．∃x＜0，x²-x＜0	B．∀x＜0，x²-x＜0
C．∃x≥0，x²-x＜0	D．∀x≥0，x²-x＜0

2022-2023学年陕西省西安三中高二（下）第二次测评数学试卷（理科）

一、选择题（本题共12小题，每小题5分，共60分）

1．已知集合A={y|y=2x-1}，B={x|y=log0.5（2-x）}，则A∩B=（ ）

2．设x∈R，向量a=（1，2），b=（x,1），c=（4，x）．则“a⊥b”是“b∥c”的（ ）

3．已知命题p：∀x≥0，x2-x≥0，则￢p为（ ）

4．随机变量X的分布列如下，则D（X）的最大值是（ ） X 0 1 P a b

5．设命题p：方程x2k+1+y23-k=1表示焦点在y轴上的椭圆；命题q：方程x2k+1+y2k-2=1表示焦点在x轴上的双曲线，若p∧q为真，则实数k的取值范围（ ）

6．某射手每次射击击中目标的概率均为P（0＜P＜1），且各次射击的结果互不影响．设随机变量X为该射手在n次射击中击中目标的次数，若E（X）=4，D（X）=43，则P的值为（ ）

7．已知a=2π∫204-x2dx,若（1-ax）2018=b0+b1x+b2x2+…+b2018x2018（x∈R），则b12+b222+…+b201822018的值为（ ）

三、解答题（本题共6小题，共70分）

1．已知集合A={y|y=2^x-1}，B={x|y=log_0.5（2-x）}，则A∩B=（　　）

2．设x∈R，向量
a
=
（
1
，
2
）
，
b
=
（
x
,
1
）
，
c
=
（
4
，
x
）
．则“
a
⊥
b
”是“
b
∥
c
”的（　　）

3．已知命题p：∀x≥0，x²-x≥0，则￢p为（　　）

4．随机变量X的分布列如下，则D（X）的最大值是（　　）

X 0 1

P a b

5．设命题p：方程
x
2
k
+
1
+
y
2
3
-
k
=
1
表示焦点在y轴上的椭圆；命题q：方程
x
2
k
+
1
+
y
2
k
-
2
=
1
表示焦点在x轴上的双曲线，若p∧q为真，则实数k的取值范围（　　）

6．某射手每次射击击中目标的概率均为P（0＜P＜1），且各次射击的结果互不影响．设随机变量X为该射手在n次射击中击中目标的次数，若
E
（
X
）
=
4
，
D
（
X
）
=
4
3
，则P的值为（　　）

7．已知a=
2
π
∫
2
0
4
-
x
2
dx,若（1-ax）²⁰¹⁸=b₀+b₁x+b₂x²+…+b₂₀₁₈x²⁰¹⁸（x∈R），则
b
1
2
+
b
2
2
2
+
…
+
b
2018
2
2018
的值为（　　）