2022-2023学年山东省日照市东港区新营中学九年级（上）期中数学试卷
发布：2024/9/1 3:0:8
一、选择题（本题共12小题，每小题3分，共36分）
-
1．如图是“光盘行动”的宣传海报（部分），图中餐盘与筷子可看成直线和圆的位置关系是（ ）组卷：446引用：12难度：0.7 -
2．下列有关圆的一些结论：①平分弦的直径垂直于弦；②三点确定一个圆；③平分弧的直径垂直于弧所对的弦；④同弧或等弧所对的弦相等，其中正确的有（ ）
组卷：301引用：5难度：0.6 -
3．如图所示，一副普通扑克牌中的13张属黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，则抽出的牌点数是3的数的概率为（ ）组卷：76引用：3难度：0.7 -
4．将圆心角为90°，面积为4πcm2的扇形围成一个圆锥的侧面，则所围成的圆锥的底面半径为（ ）
组卷：1850引用：50难度：0.9 -
5．点P到⊙O的最近点的距离为2cm,最远点的距离为7cm,则⊙O的半径是（ ）
组卷：660引用：3难度：0.6 -
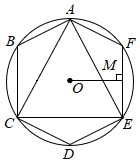6．如图，已知⊙O的内接正六边形ABCDEF的边心距OM=1，则该圆的内接正三角形ACE的面积为（ ）组卷：726引用：6难度：0.5 -
7．如图，AB，CD是⊙O的弦，延长AB，CD相交于点P．已知∠P=30°，∠AOC=80°，则BD所对的圆心角的度数是（ ）组卷：2495引用：10难度：0.7
三、解答题（共68分）
-
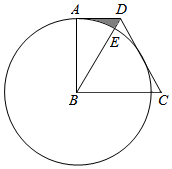21．如图，在四边形ABCD中，∠ABC=90°，AD∥BC，CB=CD，连接BD，以点B为圆心，BA长为半径作⊙B，交BD于点E．
（1）试判断CD与⊙B的位置关系，并说明理由．
（2）若AB=6，∠BDC=60°，求图中阴影部分的面积．组卷：100引用：2难度：0.5 -
22．【问题呈现】阿基米德折弦定理：
如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，点M是的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=DB+BA．下面是运用“截长法”证明CD=DB+BA的部分证明过程．ˆABC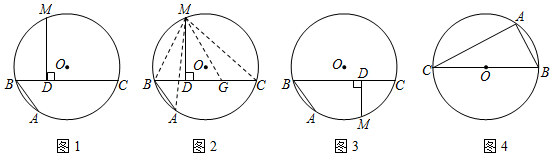
证明：如图2，在CD上截取CG=AB，连接MA、MB、MC和MG．
∵M是的中点，ˆABC
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程，分别写出下列步骤的理由：
①，
②，
③；
【理解运用】如图1，AB、BC是⊙O的两条弦，AB=4，BC=6，点M是的中点，MD⊥BC于点D，则BD=；ˆABC
【变式探究】如图3，若点M是的中点，【问题呈现】中的其他条件不变，判断CD、DB、BA之间存在怎样的数量关系？并加以证明．ˆAC
【实践应用】根据你对阿基米德折弦定理的理解完成下列问题：
如图4，BC是⊙O的直径，点A圆上一定点，点D圆上一动点，且满足∠DAC=45°，若AB=6，⊙O的半径为5，求AD长．组卷：958引用：3难度：0.3
