【问题呈现】阿基米德折弦定理:
如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是ˆABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
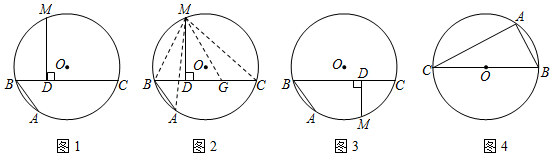
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是ˆABC的中点,
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程,分别写出下列步骤的理由:
①相等的弧所对的弦相等相等的弧所对的弦相等,
②同弧所对的圆周角相等同弧所对的圆周角相等,
③有两组边及其夹角分别对应相等的两个三角形全等有两组边及其夹角分别对应相等的两个三角形全等;
【理解运用】如图1,AB、BC是⊙O的两条弦,AB=4,BC=6,点M是ˆABC的中点,MD⊥BC于点D,则BD=11;
【变式探究】如图3,若点M是ˆAC的中点,【问题呈现】中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
【实践应用】根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=6,⊙O的半径为5,求AD长.
ˆ
ABC
ˆ
ABC
ˆ
ABC
ˆ
AC
【考点】圆的综合题.
【答案】相等的弧所对的弦相等;同弧所对的圆周角相等;有两组边及其夹角分别对应相等的两个三角形全等;1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/8 8:0:9组卷:958引用:3难度:0.3
相似题
-
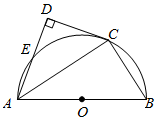 1.如图,AB为⊙O的直径,点C是⊙O上一点.CD与⊙O相切于点C,过点A作AD⊥DC,交半圆O于点E.连接AC,BC.
1.如图,AB为⊙O的直径,点C是⊙O上一点.CD与⊙O相切于点C,过点A作AD⊥DC,交半圆O于点E.连接AC,BC.
(1)求证:AC是∠DAB的角平分线;
(2)若AD=2,AB=3,求AC的长;
(3)若AE=2DE.试判断以O,A,E,C为顶点的四边形的形状为.发布:2025/5/25 1:0:1组卷:395引用:2难度:0.3 -
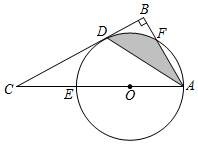 2.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
2.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
(1)求证:①BC是⊙O的切线;
②CD2=CE•CA;
(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.发布:2025/5/25 1:0:1组卷:3655引用:17难度:0.4 -
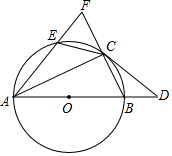 3.如图,四边形ABCE内接于⊙O,AB是⊙O的直径,点D在AB的延长线上,延长AE交BC的延长线于点F,点C是BF的中点,∠BCD=∠CAE.
3.如图,四边形ABCE内接于⊙O,AB是⊙O的直径,点D在AB的延长线上,延长AE交BC的延长线于点F,点C是BF的中点,∠BCD=∠CAE.
(1)求证:CD是⊙O的切线;
(2)求证:△CEF是等腰三角形;
(3)若BD=1,CD=2,求cos∠CBA的值及EF的长.发布:2025/5/25 1:0:1组卷:818引用:7难度:0.1


