2022-2023学年哈尔滨市六中高一(下)月考数学试卷(4月份)
发布:2024/5/16 8:0:9
一、单选题:本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项符合题目要求的.
-
1.已知向量
,a=(-1,2),则b=(0,1)的坐标为( )a-2b组卷:114引用:3难度:0.8 -
2.在△ABC中,若
,则△ABC的形状为( )|AB|=|AC|=|AB-AC|组卷:41引用:2难度:0.7 -
3.在△ABC中,角A,B,C所对的边分别为a,b,c,若A:B:C=3:2:1,则a:b:c=( )
组卷:152引用:4难度:0.8 -
4.下列命题:
①若,则|a|=|b|;a=b
②的充要条件是a=b且|a|=|b|a∥b
③若,则a∥b,b∥c;a∥c
④若A,B,C,D是不共线的四点,则是四边形ABCD为平行四边形的充要条件.AB=DC
其中,真命题的个数是( )组卷:194引用:3难度:0.9 -
5.已知O,N,P在△ABC所在的平面内,且
,|OA|=|OB|=|OC|,NA+NB+NC=0,则O,N,P分别是△ABC的( )PA•PB=PB•PC=PA•PC组卷:131引用:1难度:0.8 -
6.若向量
=(x,2),a=(2,3),b=(2,-4),且c∥a,则c在a上的投影向量为( )b组卷:347引用:9难度:0.8 -
7.△ABC中A,B,C的对边分别是a,b,c,若
=sinAsinB,(b+c+a)(b+c-a)=3bc,则△ABC的形状为( )ac组卷:249引用:14难度:0.9
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
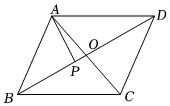 21.如图,在平行四边形ABCD中,AP⊥BD,垂足为P.
21.如图,在平行四边形ABCD中,AP⊥BD,垂足为P.
(1)若,求AP的长;AP•AC=8
(2)设||=3,|AB|=4,∠BAC=AC,π3=xAP+yAB,求x和y的值.AC组卷:288引用:4难度:0.5 -
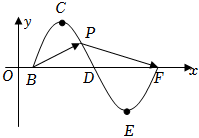 22.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,点B,D,F为f(x)与x轴的交点,点C,E分别为f(x)的最高点和最低点,而函数f(x)的相邻两条对称轴之间的距离为2,且其在处取得最小值.x=-12
22.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,点B,D,F为f(x)与x轴的交点,点C,E分别为f(x)的最高点和最低点,而函数f(x)的相邻两条对称轴之间的距离为2,且其在处取得最小值.x=-12
(1)求参数ω和φ的值;
(2)若A=1,求向量与向量2BC-CD夹角的余弦值;BC+3CD
(3)若点P为函数f(x)图象上的动点,当点P在C,E之间运动时,•BP≥1恒成立,求A的取值范围.PF组卷:438引用:11难度:0.3


