2022-2023学年福建省龙岩市高二（下）期末数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个符合题目要求请把答案填涂在答题卡上．

• 1．已知函数f（x）=cosx-4x,则

  f

  ′

  （

  π

  2

  ）

  =（　　）

  A．-5

  B．-10

  C．-3

  D．-6
  组卷：48引用：1难度：0.8

  解析

• 2．投掷一个骰子，记事件A={1，2，4，6}，B={1，2，3，4，5}，则P（B|A）=（　　）

  A． 1 4

  B． 4 5

  C． 3 5

  D． 3 4
  组卷：33引用：1难度：0.7

  解析

• 3．函数y=-x⁴+2x²+1的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：72引用：1难度：0.8

  解析

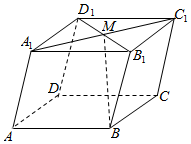• 4．如图，在平行六面体ABCD-A₁B₁C₁D₁中，M为A₁C₁，B₁D₁的交点．若

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则向量

  BM

  =（　　）

  A．- 1 2 a + 1 2 b + c

  B． 1 2 a + 1 2 b + c

  C．- 1 2 a - 1 2 b + c

  D． 1 2 a - 1 2 b + c
  组卷：1909引用：49难度：0.7

  解析

• 5．已知直三棱柱ABC-A₁B₁C₁中，

  ∠

  ABC

  =

  2

  π

  3

  ，AB=BC=2，CC₁=1，D是A₁C₁的中点，则异面直线BA₁与CD所成角的余弦值为（　　）

  A． 5 5

  B． 2 5 5

  C． 10 5

  D． 15 5
  组卷：82引用：2难度：0.5

  解析

• 6．已知甲、乙盒子各装有形状大小完全相同的小球，其中甲盒子内有2个红球，1个白球；乙盒子内有3个红球，2个白球．若第一次先从甲盒子内随机抽取1个球放入乙盒子中，则第二次从乙盒子中抽1个球是红球的概率为（　　）

  A． 4 9

  B． 1 2

  C． 11 18

  D． 3 5
  组卷：196引用：1难度：0.8

  解析

• 7．∀x∈R，f'（x）-f（x）=（-2x+1）e^x，f（0）=-3，则不等式f（x）＞-5e^x的解集为（　　）

  A．（-2，1）

  B．（-2，-1）

  C．（-1，1）

  D．（-1，2）
  组卷：45引用：1难度：0.6

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

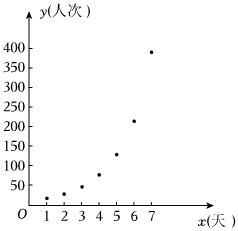• 21．三年疫情对我们的学习生活以及各个行业都产生了影响，某房地产开发公司为了回笼资金，提升销售业绩，公司旗下的某个楼盘统一推出了为期7天的优惠活动．负责人用表格记录了推出活动以后每天售楼部到访客户的人次，表格中x表示活动推出的天数，y表示每天来访的人次，根据表格绘制了以下散点图．
  

  x（天）	1	2	3	4	5	6	7
  y（人次）	12	22	42	68	132	202	392

  v	7 ∑ i = 1 y i	7 ∑ i = 1 x i y i	7 ∑ i = 1 x i v i	7 ∑ i = 1 x 2 i	e1.94	e0.575
  4.24	870	5070	134.82	140	6.96	1.78

  表中v_i=lny_i，

  v

  =

  1

  7

  7

  ∑

  i

  =

  1

  v

  i

  ．
  （1）（i）请根据散点图判断，以下两个函数模型y=a+bx与y=c•d^x（a,b,c,d均为大于零的常数）哪一个适宜作为人次y关于活动推出天数x的回归方程类型？（给出判断即可，不必说明理由）；
  （ii）根据（i）的判断结果以及表中的数据，求y关于x的回归方程．
  （2）此楼盘共有N套房，其中200套特价房，活动期间共卖出300套房，其中50套特价房，试给出N的估计值（以使得P（X=50）最大的N的值作为N的估计值，X表示卖出的300套房中特价房的数目）．
  附：对于样本（x_i，y_i）（i=1，2，…，n），其回归直线

  ̂

  y

  =

  ̂

  b

  x

  +

  ̂

  a

  的斜率和截距的最小二乘估计公式分别为：

  ̂

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ，

  ̂

  a

  =

  y

  -

  ̂

  b

  x

  ．
  组卷：55引用：1难度：0.5

  解析

• 22．已知函数f（x）=ax-lnx.
  （1）讨论f（x）的单调性；
  （2）已知g（x）=xf（x）+b,且x₁，x₂是g（x）的两个零点，x₁＜x₂，证明：x₂（ax₁-1）＜b＜x₁（ax₂-1）．
  组卷：37引用：1难度：0.6

  解析