2022-2023学年江苏省泰州二中附中九年级（上）期末数学试卷

一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

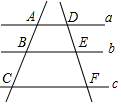• 1．如图，直线a∥b∥c,直线AC分别交a,b,c于点A，B，C：直线DF分别交a,b,c于点D，E，F．若

  AB

  BC

  =

  2

  3

  ，则

  DE

  DF

  =（　　）

  A． 2 3

  B． 2 5

  C． 3 5

  D． 3 2
  组卷：793引用：4难度：0.6

  解析

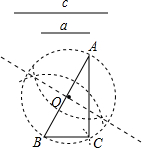• 2．数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c,一条直角边BC=a.小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（　　）

  A．勾股定理

  B．直径所对的圆周角是直角

  C．勾股定理的逆定理

  D．90°的圆周角所对的弦是直径
  组卷：1336引用：50难度：0.9

  解析

• 3．已知一个正多边形的内角是140°，则它是几边形（　　）

  A．10

  B．9

  C．8

  D．7
  组卷：421引用：7难度：0.6

  解析

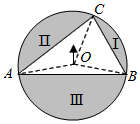• 4．如图，转盘中点A，B，C在圆上，∠A=40°，∠B=60°，让转盘绕圆心O自由转动，当转盘停止时指针指向区域Ⅲ的概率是（　　）

  A． 2 9

  B． 1 3

  C． 4 9

  D． 5 9
  组卷：239引用：2难度：0.7

  解析

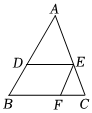• 5．如图，在△ABC中，DE∥BC，EF∥AB，记S_△ADE=16，S_△EFC=4，则S_{平行四边形DBFE}=（　　）

  A．9

  B．12

  C．16

  D．20
  组卷：609引用：3难度：0.6

  解析

• 6．在平面直角坐标系中，设函数y=ax²+（a-1）x-1（a是常数，a≠0）
  ①若a＞0，则该函数图象与x轴一定有两个交点，而且在原点两侧．
  ②无论a取何值，该函数图象必定经过两个定点．则（　　）

  A．①错误，②错误	B．①正确，②错误
  C．①错误，②正确	D．①正确，②正确
  组卷：452引用：2难度：0.6

  解析

二、填空题（本大题共有10小题，每小题3分，共30分，请把答案直接填写在答题卡相应位置上）

• 7．已知线段a=4，线段b=9，则a,b的比例中项是

  ．
  组卷：575引用：4难度：0.5

  解析

• 8．若⊙O的半径为3cm,点A与圆心O的距离为4cm,则点A与⊙O的位置关系是

  ．
  组卷：410引用：5难度：0.7

  解析

三、解答题（本大题共有10题，共102分，请在答题卡规定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

• 25．（1）如图1，D、E为等边△ABC中BC边所在直线上两点，∠DAE=120°，求证：△ABD∽△ECA；
  （2）△ADE中，∠DAE=120°，请用不含刻度的直尺和圆规在DE上求作两点B、C，点B在点C的左侧，使得△ABC为等边三角形；
  （3）在（1）的条件下，H为BC边上一点，过H作HF∥AD交AB延长线于点F，HG∥AE交AC延长线于点G，若AB=6，BD=a,∠HAE=60°，求

  HF

  HG

  的值．（用含有a的代数式表示）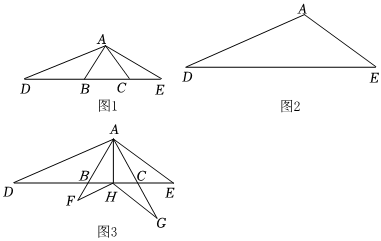
  组卷：359引用：2难度：0.1

  解析

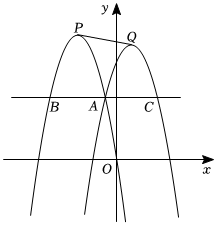• 26．在平面直角坐标系中，已知抛物线

  y

  1

  =

  -

  x

  2

  -

  6

  x

  ．
  （1）求抛物线y₁的顶点P坐标；
  （2）平移抛物线y₁得抛物线y₂，两抛物线交于点A，过点A作x轴的平行线交抛物线y₁和平移后的抛物线y₂分别为B和C（点B在点C的左侧）．
  ①平移后的抛物线y₂顶点在直线x=1上，点A的横坐标为-1，求抛物线y₂的表达式；
  ②平移后的抛物线y₂顶点在直线x=1上，点A的横坐标为m（-3＜m＜1），求BC的长；
  ③设点A的横坐标为n,BC=10，抛物线y₂的顶点为Q，设PQ²=y,求y关于n的函数表达式，并求PQ的最小值．
  组卷：449引用：2难度：0.4

  解析