当前位置：试卷中心 > 试卷详情

2022-2023学年广西桂林市高二（下）期末数学试卷

发布：2024/7/17 8:0:9

一、单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，且只有一项是符合题目要求的.

1．
1
64
是数列
1
2
、
1
4
、
1
8
、
1
16
、⋯的（　　）
A．第6项 B．第7项 C．第8项 D．第9项
组卷：213引用：4难度：0.7
解析
2．函数f（x）=e^x的导函数f′（x）=（　　）
A．e^x B．ex C．e D．x
组卷：47引用：1难度：0.7
解析
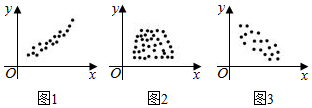3．观察下列散点图，则①正相关，②负相关，③不相关，这三句话与散点图的位置相对应的是（　　）
A．①②③ B．②③① C．②①③ D．①③②
组卷：225引用：11难度：0.9
解析
4．若函数f（x）=x²，则
lim
Δ
x
→
0
f
（
1
+
Δ
x
）
-
f
（
1
）
Δ
x
=（　　）
A．1 B．2 C．3 D．4
组卷：85引用：4难度：0.7
解析
5．某电子管正品率为
3
4
，次品率为
1
4
，现对该批电子管进行测试，那么在五次测试中恰有三次测到正品的概率是（　　）
A．
C
3
5
（
3
4
）
3
B．
C
2
5
（
1
4
）
2
C．
C
2
5
（
3
4
）
2
（
1
4
）
3
D．
C
3
5
（
3
4
）
3
（
1
4
）
2
组卷：280引用：3难度：0.7
解析
6．已知各项均为正数的等比数列{a_n}满足a₁•a₅=16，a₂=2，则公比q=（　　）
A．4 B．
5
2
C．2 D．
1
2
组卷：237引用：6难度：0.7
解析
7．某市2018年至2022年新能源汽车年销量y（单位：千台）与年份代号x的数据如下表：

年份 2019 2020 2021 2022

年份代号x 1 2 3 4

年销量y 15 20 m 35

若根据表中的数据用最小二乘法求得y关于x的经验回归直线方程为
̂
y
=
7
x
+
7
.
5
，则表中m的值为（　　）
A．25 B．28 C．30 D．32
组卷：89引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6小题，共70分.解答应给出文字说明、证明过程及演算步骤.

21．已知①2a₃=b₃+b₄；②S₂=3；③a₄=a₃+2a₂，在这三个条件中选一个，补充在下面问题中，并给出解答．
设正项等比数列{a_n}的前n项和为S_n，数列{b_n}的前n项和为T_n，_____，a₁=b₂，对∀n∈N，都有T_n=n²+2b₁n成立．
（1）求数列{a_n}，{b_n}的通项公式；
（2）若数列{a_n•b_n}的前n项和为H_n，证明H_n＞（2n-5）•2ⁿ．
组卷：17引用：1难度：0.5
解析
22．已知函数f（x）=x-ln（x+1）-sinx.
（1）求函数f（x）在区间[0，π]上的最大值；
（2）求函数f（x）零点的个数．
组卷：64引用：3难度：0.5
解析