2023-2024学年江苏省无锡市新吴区辅仁高中高一（上）质检数学试卷（一）

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知全集U={1，2，3，5}，M={1，2}，N={3，4}，（∁_UM）∪N=（　　）

  A．{4}

  B．{4，5}

  C．{3，4，5}

  D．{1，2，3，4，5}
  组卷：57引用：5难度：0.7

  解析

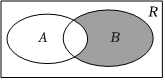• 2．设全集U=R，B={x|x²-x-2＜0}，A={x|x≤1}，则图中阴影部分对应的集合为（　　）

  A．{x|x≥1}

  B．{x|1≤x＜2}

  C．{x|x＞1}

  D．{x|1＜x＜2}
  组卷：47引用：3难度：0.8

  解析

• 3．设

  M

  =

  {

  x

  |

  x

  =

  k

  2

  ，

  k

  ∈

  Z

  }

  ，

  N

  =

  {

  x

  |

  x

  =

  k

  +

  1

  2

  ，

  k

  ∈

  Z

  }

  ，则（　　）

  A．M⊆N

  B．N⊆M

  C．M=N

  D．M∩N=∅
  组卷：177引用：2难度：0.5

  解析

• 4．十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用．后来英国数学家哈利奥特首次使用“＜”和“＞”符号，并逐渐被数学界接受，不等号的引入对不等式的发展影响深远．若a,b,c∈R，则下列命题正确的是（　　）

  A．若ab≠0且a＜b,则 1 a ＞ 1 b	B．若0＜a＜1，则a2＞a
  C．若a＞b＞0，c＞d,则ac＞bd	D．若a＜b＜0，则a2＞b2
  组卷：79引用：9难度：0.7

  解析

• 5．已知a∈R，则“a＜-1”是“

  2

  a

  -

  1

  a

  +

  1

  ＞

  1

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：31引用：5难度：0.8

  解析

• 6．设全集U={1，2，3，4，5，6}，A，B是U的两个子集，集合A={1，2，3，5}，则满足A∩B={1，2}的集合B共有（　　）

  A．4个

  B．8个

  C．6个

  D．2个
  组卷：87引用：3难度：0.7

  解析

• 7．若a＞0，b＞0，且ab=a+b+1，a+8b的最小值为（　　）

  A．15

  B． 8 + 4 2

  C．17

  D． 6 + 4 2
  组卷：115引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤.

• 21．已知关于x的不等式（kx-k²-4）（x-4）＞0，其中k∈R．
  （1）求上述不等式的解；
  （2）是否存在实数k,使得上述不等式的解集A中只有有限个整数？若存在，求出使得A中整数个数最少的k的值；若不存在，请说明理由．
  组卷：91引用：7难度：0.5

  解析

• 22．已知集合A={x|1≤x≤4}，B={x|x²-ax+a+3≤0}．
  （1）若a=-3，且m+n∈A，m-n∈B．求3m-n的取值范围；
  （2）若A∩B≠∅，求实数a的取值范围．
  组卷：32引用：1难度：0.5

  解析