当前位置：试卷中心 > 试卷详情

2022-2023学年江西省抚州市临川一中九年级（上）期中数学试卷

发布：2024/9/4 3:0:8

一、选择题(本大题共6个小题,每小题4分，共24分)。

1．矩形、正方形、菱形都具有的性质是（　　）
A．对角线互相垂直
B．对角线互相平分
C．对角线长度相等
D．一组对角线平分一组对角
组卷：479引用：9难度：0.6
解析
2．若关于x的一元二次方程（m-1）x²+2x-2=0有两个不相等的实数根，则实数m的取值范围是（　　）
A．m＜
1
2
B．m＞
1
2
C．m＞
1
2
且m≠1 D．m≠1
组卷：1061引用：11难度：0.7
解析
3．一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是（　　）
A．
1
2
B．
1
4
C．
1
6
D．
1
12
组卷：2488引用：111难度：0.9
解析
4．已知线段AB的长度为2，点C是线段AB的黄金分割点，则AC的长度为（　　）
A．
5
-
1
2
B．
3
-
5
2
C．
5
-1或3
-
5
D．
5
-
1
2
或
5
-2
组卷：654引用：10难度：0.8
解析
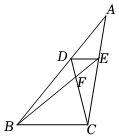5．如图，点D为△ABC边AB上任一点，DE∥BC交AC于点E，连接BE、CD相交于点F，则下列等式中不成立的是（　　）
A．
AD
DB
=
AE
EC
B．
DE
BC
=
DF
FC
C．
DE
BC
=
AE
EC
D．
EF
BF
=
AE
AC
组卷：3398引用：22难度：0.6
解析
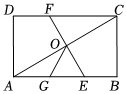6．如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB于E，点G是AE中点且∠AOG=30°，则下列结论正确的个数为（　　）
①△OGE是等边三角形；②DC=3OG；③OG=
1
2
BC；④
S
△
AOE
=
1
6
S
矩形
ABCD
．
A．1个 B．2个 C．3个 D．4个
组卷：197引用：5难度：0.6
解析

二、填空题（本大题共6个小题，每小题3分，共18分）

7．若
x
y
=
2
3
，则
3
x
+
2
y
4
y
+
3
x
=
．
组卷：52引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、（本大题共3个小题，每小题8分，共24分）

22．将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，如图①所示，∠BAB′=θ，
A
B
′
AB
=
B
′
C
′
BC
=
A
C
′
AC
=n,我们将这种变换记为[θ，n]．
（1）如图①，对△ABC作变换[60°，
3
]得到△AB′C′，则S_△AB'C：S_△ABC=

；直线BC与直线B′C′所夹的锐角为

度；
（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、C′在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；
（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．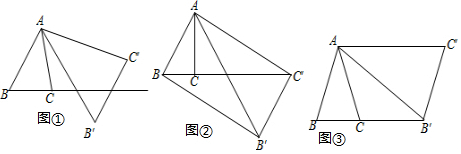
组卷：245引用：5难度：0.5
解析
23．已知：在正方形ABCD的边BC上任取一点F，连接AF，一条与AF垂直的直线l（垂足为点P）沿AF方向，从点A开始向下平移，交边AB于点E．

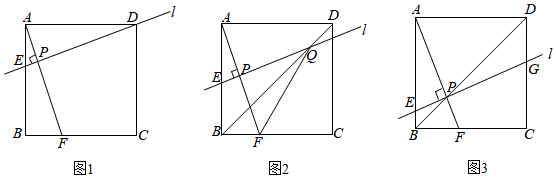
（1）当直线l经过正方形ABCD的顶点D时，如图1所示．求证：AE=BF；
（2）当直线l经过AF的中点时，与对角线BD交于点Q，连接FQ，如图2所示．求∠AFQ的度数；
（3）直线l继续向下平移，当点P恰好落在对角线BD上时，交边CD于点G，如图3所示．设AB=2，BF=x,DG=y,求y与x之间的关系式．
组卷：2673引用：3难度：0.1
解析