2023-2024学年重庆八中高二（上）月考数学试卷（9月份）

一、选择题：本题共8小题，每小题5分，共计40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知向量

  a

  =（2，4），

  b

  =（-1，1），则2

  a

  -

  b

  =（　　）

  A．（5，7）

  B．（5，9）

  C．（3，7）

  D．（3，9）
  组卷：3981引用：69难度：0.9

  解析

• 2．已知直线l₁：x-3y+2=0，l₂：3x-ay-1=0，若l₁⊥l₂，则实数a的值为（　　）

  A．1

  B． 1 2

  C． - 1 2

  D．-1
  组卷：64引用：1难度：0.8

  解析

• 3．已知m是实常数，若方程x²+y²+2x+4y+m=0表示的曲线是圆，则m的取值范围为（　　）

  A．（-∞，20）

  B．（-∞，5）

  C．（5，+∞）

  D．（20，+∞）
  组卷：1468引用：11难度：0.8

  解析

• 4．设a,b为两条直线，α，β为两个平面，下列四个命题中，正确的命题是（　　）

  A．若a,b与α所成的角相等，则α∥b

  B．若a∥α，b∥β，α∥β，则a∥b

  C．若a⊂α，b⊂β，α∥b,则α∥β

  D．若a⊥α，b⊥β，α⊥β，是a⊥b
  组卷：997引用：56难度：0.5

  解析

• 5．直线y=kx+3与圆（x-3）²+（y-2）²=4相交于M、N两点，若

  |

  MN

  |

  =

  2

  3

  ，则k等于（　　）

  A．0

  B． - 2 3

  C． - 2 3 或 0

  D． - 3 4 或 0
  组卷：226引用：7难度：0.9

  解析

• 6．过点P（1，3）作直线l,若l经过点A（a,0）和B（0，b），且a,b均为正整数，则这样的直线l可以作出（　　）

  A．1条

  B．2条

  C．3条

  D．无数条
  组卷：215引用：6难度：0.6

  解析

• 7．已知长方体ABCD-A₁B₁C₁D₁中，AA₁=AB=2，若棱AB上存在点P，使得D₁P⊥PC，则AP的取值范围是（　　）

  A．[1，2）

  B． （ 1 ， 2 ]

  C．（0，1]

  D．（0，2）
  组卷：508引用：9难度：0.9

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

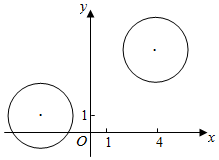• 21．在平面直角坐标系xOy中，已知圆

  C

  1

  ：

  （

  x

  +

  3

  ）

  2

  +

  （

  y

  -

  1

  ）

  2

  =

  4

  和圆

  C

  2

  ：

  （

  x

  -

  4

  ）

  2

  +

  （

  y

  -

  5

  ）

  2

  =

  4

  ．
  （1）若直线l过点A（-1，0），且与圆C₁相切，求直线l的方程；
  （2）设P为直线

  x

  =

  -

  3

  2

  上的点，满足：过点P的无穷多对互相垂直的直线l₁和l₂，它们分别与圆C₁和圆C₂相交，且直线l₁被圆C₁截得的弦长与直线l₂被圆C₂截得的弦长相等．试求满足条件的点P的坐标．
  组卷：144引用：8难度：0.3

  解析

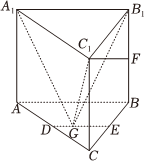• 22．如图，已知直三棱柱A₁B₁C₁-ABC中，∠ABC=90°且AB=BC=BB₁=2，D、E、F分别为AC、BC、B₁B的中点，G为线段DE上一动点．
  （1）求C₁F与平面A₁B₁C₁所成角的正切值；
  （2）证明：C₁F⊥A₁G；
  （3）求锐二面角C₁-A₁G-B₁的余弦值的最大值．
  组卷：210引用：4难度：0.6

  解析