2022-2023学年江苏省镇江市丹阳高级中学高一（下）第二次月考数学试卷

一、单选题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是合题目要求的。）

• 1．

  AD

  +

  DC

  -

  AB

  等于（　　）

  A． BC

  B． AD

  C． AB

  D． DA
  组卷：360引用：4难度：0.8

  解析

• 2．复平面内，复数

  3

  -

  i

  1

  +

  i

  2023

  对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：82引用：4难度：0.8

  解析

• 3．下列各式中，值为

  1

  2

  的是（　　）

  A． 2 2 （ cos 15 ° - sin 15 ° ）	B． co s 2 π 12 - si n 2 π 12
  C． tan 22 . 5 ° 1 - tan 2 22 . 5 °	D．sin15°cos15°
  组卷：138引用：6难度：0.7

  解析

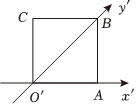• 4．如图，一个水平放置的平面图形的直观图是边长为2的正方形，则原图形的周长是（　　）

  A．16

  B．12

  C． 4 + 8 2

  D． 4 + 4 2
  组卷：386引用：9难度：0.9

  解析

• 5．在△ABC中，若acosA=bcosB，则△ABC的形状一定是（　　）

  A．等腰直角三角形	B．直角三角形
  C．等腰三角形	D．等腰或直角三角形
  组卷：1433引用：17难度：0.7

  解析

• 6．在正方体ABCD-A₁B₁C₁D₁中，E是C₁D₁的中点，则异面直线DE与AC所成角的余弦值是（　　）

  A．0

  B． 1 2

  C． 3 10 10

  D． 10 10
  组卷：519引用：7难度：0.5

  解析

• 7．函数

  f

  （

  x

  ）

  =

  3

  sin

  2

  x

  +

  2

  co

  s

  2

  x

  ，若f（x₁）•f（x₂）=-3，则|x₁+x₂|的最小值是（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  组卷：91引用：3难度：0.7

  解析

四、解答题。(本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）

• 21．老王拟将自家一块直角三角形地按如图规划成3个功能区：△BNC区域规划为枇杷林和放养走地鸡，△CMA区域规划为民宿供游客住宿及餐饮，△MNC区域规划为鱼塘养鱼供垂钓．为安全起见，在鱼塘△MNC周围筑起护栏，已知AC=40m,BC=40

  3

  m,AC⊥BC，∠MCN=30°．
  （1）若AM=20m,求护栏的长度（即△MNC的周长）；
  （2）若鱼塘△MNC的面积是民宿△CMA面积的

  3

  倍，求∠ACM．
  组卷：66引用：5难度：0.4

  解析

• 22．在锐角△ABC中，角A，B，C所对的边分别是a,b,c,已知b=2，

  a

  b

  =

  3

  3

  sinC+cosC．
  （1）求角B；
  （2）若M是△ABC内的一动点，且满足

  BM

  =

  MA

  +

  MC

  ，则|

  BM

  |是否存在最大值？若存在，请求出最大值及取最大值的条件；若不存在，请说明理由；
  （3）若D是△ABC中AC上的一点，且满足

  BA

  •

  BD

  |

  BA

  |

  =

  BD

  •

  BC

  |

  BC

  |

  ，求AD：DC的取值范围．
  组卷：344引用：6难度：0.3

  解析