2022-2023学年浙江省嘉兴市八年级（下）期末数学试卷

一、选择题（每小题有4个选项，其中有且只有一个正确，请把正确选项的编码填入答题卷的相应空格，每小题3分，共30分）

• 1．下列方程属于一元二次方程的是（　　）

  A．x+y=1

  B．x2+x=0

  C． x + 1 x 2 = 4

  D．1-2x=x
  组卷：183引用：3难度：0.8

  解析

• 2．下列折纸图案属于中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：59引用：2难度：0.5

  解析

• 3．平行四边形不一定具有的特征是（　　）

  A．对角相等

  B．对边相等

  C．对角线相等

  D．对边平行
  组卷：107引用：5难度：0.9

  解析

• 4．下列运算结果正确的是（　　）

  A． 10 ÷ 5 = 5

  B． 9 =± 3

  C． （ - 2 ） 2 = 2

  D． 2 + 3 = 5
  组卷：58引用：3难度：0.7

  解析

• 5．用配方法解方程x²-4x-5=0时，原方程应变形为（　　）

  A．（x-2）2=1

  B．（x-2）2=9

  C．（x-4）2=21

  D．（x-4）2=11
  组卷：390引用：11难度：0.7

  解析

• 6．用反证法证明“在△ABC中，若AB=AC，则∠B=∠C”时，则应假设（　　）

  A．∠A=∠B

  B．∠B≠∠C

  C．AB≠AC

  D．BC=AC
  组卷：111引用：4难度：0.7

  解析

• 7．质检员随机抽取四家公司生产的相同数量的同种零件，经整理后得到如下数据（零件尺寸合格范围为6.50±0.05mm），零件生产精度更高的公司是（　　）
  

  公司	甲	乙	丙	丁
  平均尺寸	6.49mm	6.51mm	6.56mm	6.49mm
  方差	1.22	2.77	1.00	1.85

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：33引用：1难度：0.6

  解析

• 8．一个多边形剪去一个角后得到一个新的多边形，则关于这两个多边形，下列量中一定没有发生变化的是（　　）

  A．内角度数

  B．内角和度数

  C．对角线条数

  D．外角和度数
  组卷：225引用：2难度：0.5

  解析

三、解答题（本题有8小题，第17～22题每题6分，第23、24题每题8分，共52分）

• 23．定义一种新运算：对于任意非零实数m和n,

  m

  ※

  n

  =

  n m （ m ＜ n ）

  m n （ m ≥ n ）

  ，例如：

  3

  ※

  2

  =

  3

  2

  ，

  -

  2

  ※

  3

  =

  -

  3

  2

  ，请回答下列问题：
  （1）计算

  2

  ※

  2

  ；
  （2）解方程：（x²+2x+2）※1=2；
  （3）直接写出不等式2※x＞4※x的解．
  组卷：156引用：2难度：0.5

  解析

• 24．如图，DE是△ABC的中位线，点M为射线ED上的一个动点（不与点E重合），作MF∥AC交AB边于点F，连结EF．
  （1）如图1，当点M与点D重合时，求证：四边形CEFM是平行四边形；
  （2）如图2，∠B=45°，BC=4，点M在线段ED上运动，当四边形CEFM是菱形时，BF=2AF，求菱形CEFM的面积；
  （3）如图3，∠B=45°，在ED延长线上（可以与点D重合）存在一点M，使得四边形CEFM为矩形，求∠ACB的度数范围．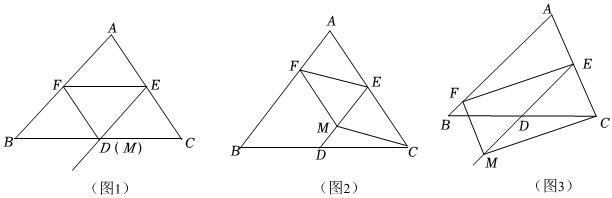
  组卷：511引用：2难度：0.5

  解析