2021-2022学年江苏省淮安市盱眙县马坝高级中学高二（下）期中数学试卷

一、单项选择题（本大题共8题，每小题5分，共计40分.每小题列出的四个选项中只有一项是最符合题目要求的）

• 1．空间直角坐标系中，已知A（1，-2，3），B（3，2，-5），则线段AB的中点为（　　）

  A．（-1，-2，4）

  B．（-2，0，1）

  C．（2，0，-2）

  D．（2，0，-1）
  组卷：379引用：4难度：0.9

  解析

• 2．由数字3，4，5组成的无重复数字的整数中，偶数的个数为（　　）

  A．15

  B．12

  C．10

  D．5
  组卷：4引用：3难度：0.7

  解析

• 3．在桥牌比赛中，发给4名参赛者每人一手由52张牌的四分之一（即13张牌）组成的牌，一名参赛者可能得到的不同的牌为（　　）

  A．4×13种

  B．134种

  C． A 13 52 种

  D． C 13 52 种
  组卷：3引用：1难度：0.7

  解析

• 4．已知

  a

  =

  （

  1

  ，

  2

  ，-

  y

  ）

  ，

  b

  =

  （

  x

  ,

  1

  ，

  2

  ）

  ，且

  （

  a

  +

  2

  b

  ）

  ∥

  （

  2

  a

  -

  b

  ）

  ，则（　　）

  A． x = 1 3 ， y = 1

  B． x = 1 2 ， y = - 4

  C． x = 2 ， y = - 1 4

  D．x=1，y=-1
  组卷：1464引用：39难度：0.9

  解析

• 5．二项式（2x-y）⁸的展开式中第3项的二项式系数为（　　）

  A．-56

  B．56

  C．-28

  D．28
  组卷：250引用：5难度：0.7

  解析

• 6．若x²+（x+1）⁷=a₀+a₁（x+2）+a₂（x+2）²+…+a₇（x+2）⁷，则a₂=（　　）

  A．22

  B．19

  C．-20

  D．-19
  组卷：486引用：3难度：0.7

  解析

• 7．已知空间四边形OABC，其对角线是OB，AC，M，N分别是对边OA，BC的中点，点G在线段MN上，且MG=3GN，用基底向量

  OA

  ，

  OB

  ，

  OC

  表示向量

  OG

  应是（　　）

  A． OG = 1 8 OA + 3 8 OB + 3 8 OC	B． OG = 1 8 OA - 3 8 OB + 3 8 OC
  C． OG = 1 6 OA + 1 3 OB + 1 3 OC	D． OG = 1 6 OA - 1 3 OB + 1 3 OC
  组卷：620引用：10难度：0.9

  解析

四、解答题（本大题共6题，计70分，每题需写出必要的解题过程或文字说明）

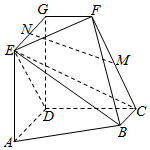• 21．如图，AD∥BC且AD=2BC，AD⊥CD，EG∥AD且EG=AD，CD∥FG且CD=2FG，DG⊥平面ABCD，DA=DC=DG=2．
  （1）若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；
  （2）求二面角E一BC一F的正弦值；
  （3）求直线AD到平面EBC的距离．
  组卷：258引用：4难度：0.6

  解析

• 22．已知

  F

  （

  n

  ）

  =

  a

  1

  +

  a

  2

  C

  1

  n

  +

  ⋯

  +

  a

  r

  C

  r

  -

  1

  n

  +

  ⋯

  +

  a

  n

  +

  1

  C

  n

  n

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）若a_n=2n-1，求F（5）；
  （2）若

  a

  n

  =

  7

  n

  -

  1

  ，求F（20）除以9的余数．
  组卷：8引用：1难度：0.5

  解析