当前位置：试卷中心 > 试卷详情

2022-2023学年河南省鹤壁市浚县一中高二（上）开学数学试卷

发布：2024/7/18 8:0:9

一、单项选择题（本题共12小题，每小题5分，共60分。在每小题鉿出的四个选项中，只有一个选项是符合题目要求的）

1．若方程
x
2
2
+
m
-
y
2
2
-
m
=
1
表示双曲线，则m的取值范围是（　　）
A．-2＜m＜2 B．m＞-2 C．m≥0 D．m≥2
组卷：313引用：9难度：0.8
解析
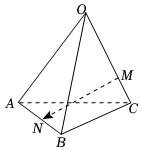2．如图，空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在线段OC上，且OM=2MC，点N为AB中点，则
MN
=（　　）
A．
1
2
a
+
1
2
b
-
2
3
c
B．
1
2
a
+
1
2
b
-
1
2
c
C．
1
2
a
-
2
3
b
+
1
2
c
D．-
2
3
a
+
1
2
b
+
1
2
c
组卷：224引用：7难度：0.8
解析
3．方程（3x-y+1）（y-
1
-
x
2
）=0表示的曲线为（　　）
A．两条线段 B．一条直线和半个圆
C．一条线段和半个圆 D．一条射线和半个圆
组卷：50引用：1难度：0.8
解析
4．唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在位置为B（2，4），若将军从点A（-2，0）处出发，河岸线所在直线方程为x-2y+8=0，则“将军饮马”的最短总路程为（　　）
A．
4
65
5
B．10 C．
10
2
D．
4
2
组卷：352引用：5难度：0.8
解析
5．已知双曲线的左、右焦点分别为F₁，F₂，过F₁的直线与双曲线的左支交于A，B两点，线段AB的长为5．若2a=8，那△ABF₂的周长是（　　）
A．16 B．18 C．21 D．26
组卷：37引用：3难度：0.8
解析
6．已知圆C₁：x²+y²-2
3
x
-
4
y
+
6
=
0
，C₂：x²+y²-6y=0，则两圆的位置关系为（　　）
A．外离 B．外切 C．相交 D．内切
组卷：413引用：18难度：0.9
解析
7．已知点F₁（-1，0），F₂（1，0），动点P到直线x=2的距离为d,
|
P
F
2
|
d
=
2
2
，则（　　）
A．点P的轨迹是圆
B．点P的轨迹曲线的离心率等于
1
2
C．点P的轨迹方程为
x
2
2
+
y
2
=
1
D．△PF₁F₂的周长为定值
4
2
组卷：76引用：6难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共6大题，共70分）

21．在如图所示的几何体中，四边形ABCD为矩形，AF⊥平面ABCD，EF∥AB，AD=2，AB=AF=2EF=1，点P为棱DF的中点．
（Ⅰ）求证：BF∥平面APC；
（Ⅱ）求直线DE与平面BCF所成角的正弦值；
（Ⅲ）求点E到平面APC的距离．
组卷：192引用：5难度：0.5
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=l（a＞b＞0）的离心率e=
3
2
，且圆x²+y²=2过椭圆C的上、下顶点．
（1）求椭圆C的方程；
（2）若直线l的斜率为
1
2
，且直线l与椭圆C相交于P，Q两点，点P关于原点的对称点为E，点A（-2，1）是椭圆C上一点，若直线AE与AQ的斜率分别为k_AE，k_AQ．
证明：k_AE+k_AQ为定值，并求出此定值．
组卷：49引用：3难度：0.6
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． 1 2 a + 1 2 b - 2 3 c	B． 1 2 a + 1 2 b - 1 2 c
C． 1 2 a - 2 3 b + 1 2 c	D．- 2 3 a + 1 2 b + 1 2 c

A．两条线段	B．一条直线和半个圆
C．一条线段和半个圆	D．一条射线和半个圆

2022-2023学年河南省鹤壁市浚县一中高二（上）开学数学试卷

一、单项选择题（本题共12小题，每小题5分，共60分。在每小题鉿出的四个选项中，只有一个选项是符合题目要求的）

1．若方程x22+m-y22-m=1表示双曲线，则m的取值范围是（ ）

2．如图，空间四边形OABC中，OA=a，OB=b，OC=c，点M在线段OC上，且OM=2MC，点N为AB中点，则MN=（ ）

3．方程（3x-y+1）（y-1-x2）=0表示的曲线为（ ）

5．已知双曲线的左、右焦点分别为F1，F2，过F1的直线与双曲线的左支交于A，B两点，线段AB的长为5．若2a=8，那△ABF2的周长是（ ）

6．已知圆C1：x2+y2-23x-4y+6=0，C2：x2+y2-6y=0，则两圆的位置关系为（ ）

7．已知点F1（-1，0），F2（1，0），动点P到直线x=2的距离为d,|PF2|d=22，则（ ）

三、解答题（本题共6大题，共70分）

21．在如图所示的几何体中，四边形ABCD为矩形，AF⊥平面ABCD，EF∥AB，AD=2，AB=AF=2EF=1，点P为棱DF的中点．（Ⅰ）求证：BF∥平面APC；（Ⅱ）求直线DE与平面BCF所成角的正弦值；（Ⅲ）求点E到平面APC的距离．

1．若方程
x
2
2
+
m
-
y
2
2
-
m
=
1
表示双曲线，则m的取值范围是（　　）

2．如图，空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在线段OC上，且OM=2MC，点N为AB中点，则
MN
=（　　）

3．方程（3x-y+1）（y-
1
-
x
2
）=0表示的曲线为（　　）

5．已知双曲线的左、右焦点分别为F₁，F₂，过F₁的直线与双曲线的左支交于A，B两点，线段AB的长为5．若2a=8，那△ABF₂的周长是（　　）

6．已知圆C₁：x²+y²-2
3
x
-
4
y
+
6
=
0
，C₂：x²+y²-6y=0，则两圆的位置关系为（　　）

7．已知点F₁（-1，0），F₂（1，0），动点P到直线x=2的距离为d,
|
P
F
2
|
d
=
2
2
，则（　　）

21．在如图所示的几何体中，四边形ABCD为矩形，AF⊥平面ABCD，EF∥AB，AD=2，AB=AF=2EF=1，点P为棱DF的中点．
（Ⅰ）求证：BF∥平面APC；
（Ⅱ）求直线DE与平面BCF所成角的正弦值；
（Ⅲ）求点E到平面APC的距离．