2022-2023学年江苏省扬州市高邮市高一（上）期中数学试卷

一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题要求的）

• 1．已知幂函数f（x）=x^α的图象过点（4，2），则α的值为（　　）

  A． 1 2

  B．- 1 2

  C． 2

  D．- 2
  组卷：448引用：3难度：0.9

  解析

• 2．下列对应是集合A到集合B的函数的是（　　）

  A．A=B=R，f：x→y=1	B．A=Z，B=Q， f ： x → y = 1 x
  C．A=B=N*，f：x→y=|x-3|	D．A=[0，+∞），B=R， f ： x → y =± x
  组卷：105引用：2难度：0.8

  解析

• 3．已知集合U=R，

  A

  =

  {

  x

  |

  1

  x

  ＜

  1

  }

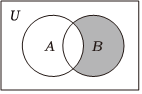  ，B={x||x|＜1}，则图中阴影部分所表示的集合是（　　）

  A．[0，1）

  B．（0，1）

  C．（-1，1）

  D．（-1，1]
  组卷：10引用：3难度：0.7

  解析

• 4．已知函数

  f

  （

  x

  ）

  =

  2 x + 1 ， x ＜ 2

  - x 2 + ax , x ≥ 2

  ，若f[f（1）]=-6，则实数a的值为（　　）

  A．-3

  B．3

  C．-1

  D．1
  组卷：35引用：4难度：0.7

  解析

• 5．函数

  f

  （

  x

  ）

  =

  ax

  +

  b

  （

  x

  +

  c

  ）

  2

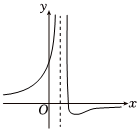  的图像如图所示，则下列结论成立的是（　　）

  A．a＞0，b＞0，c＞0	B．a＜0，b＞0，c＞0
  C．a＜0，b＞0，c＜0	D．a＜0，b＜0，c＜0
  组卷：32引用：3难度：0.7

  解析

• 6．大西洋鲑鱼每年都要逆流而上，游回到自己出生的淡水流域产卵．记鲑鱼的游速为v（单位：m/s），鲑鱼的耗氧量的单位数为Q，研究发现

  v

  =

  kln

  Q

  100

  （

  k

  ＞

  0

  ）

  ，当v=1.5m/s时，鲑鱼的耗氧量的单位数为51200，则当v=0.5m/s时，鲑鱼的耗氧量的单位数为（　　）

  A．400

  B．800

  C．1600

  D．3200
  组卷：17引用：2难度：0.6

  解析

• 7．已知定义在R上的奇函数f（x）在（0，+∞）上单调递增，且f（2）=0，则满足（x-1）•f（x-1）≤0的x的取值范围为（　　）

  A．[-1，3]	B．[-1，1）∪（1，3]
  C．（-∞，-1]∪[3，+∞）	D．（-∞，-1]∪[3，+∞）∪{1}
  组卷：41引用：2难度：0.6

  解析

四、解答题：

• 21．已知

  f

  （

  x

  ）

  =

  2

  x

  +

  m

  -

  2

  2

  x

  +

  1

  （m∈R）为奇函数；
  （1）求m的值；
  （2）判断函数f（x）的单调性，并利用函数单调性的定义证明；
  （3）若存在实数a,b（a＜b），使得f（x）在区间[a,b]上的值域为[λ+2^a，λ+2^b]，求实数λ的取值范围．
  
  组卷：46引用：2难度：0.5

  解析

• 22．已知函数f（x）=x²-ax-2．
  （1）求证：不论a取何值，函数f（x）总存在零点．
  （2）若对于任意的x∈[-1，1]，都有f（x）≥1-a²，求实数a的取值范围．
  （3）对于给定的正数a,存在一个最大的正数l（a），使得在整个区间[0，1（a）]上，不等式|f（x）|＜3恒成立，求l（a）的表达式．
  组卷：32引用：1难度：0.5

  解析