当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省南京师大附中江宁分校九年级（上）第一次月考数学试卷

发布：2024/9/1 8:0:8

一.选择题（共6小题，每小题2分，共12分）

1．把方程x²-10x-5=0变形为（x+h）²=k的形式可以是（　　）
A．（x-5）²=30 B．（x-5）²=5 C．（x+5）²=5 D．（x+5）²=30
组卷：531引用：8难度：0.6
解析
2．下列一元二次方程中，有两个相等的实数根的是（　　）
A．x²+1=0 B．x²+1=2x C．x²-2x=0 D．x²-2x=3
组卷：352引用：4难度：0.7
解析
3．已知一元二次方程x²-8x+15=0的两个根分别是Rt△ABC的两边长，则第3条边长（　　）
A．3 B．4或5 C．3或5 D．4或
34
组卷：140引用：4难度：0.9
解析
4．若⊙O的半径为4，圆心O到直线l的距离为5，则直线l与⊙O的位置关系是（　　）
A．相交 B．相切 C．相离 D．无法确定
组卷：706引用：12难度：0.9
解析
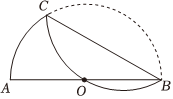5．如图，在半圆ACB中，AB=6，将半圆ACB沿弦BC所在的直线折叠，若弧BC恰好过圆心O，则BC的长是（　　）
A．
3
3
B．π C．2π D．4 π
组卷：1345引用：4难度：0.5
解析
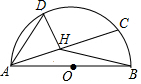6．如图，AB是半圆O的直径，点D在半圆O上，AB=2
61
，AD=10，C是弧BD上的一个动点，连接AC，过D点作DH⊥AC于H，连接BH，在点C移动的过程中，BH的最小值是（　　）
A．5 B．6 C．7 D．8
组卷：4690引用：11难度：0.1
解析

二.填空题（共10小题，每小题2分，共20分）

7．当x=
时，分式
x
2
-
9
x
+
3
的值为零．
组卷：5177引用：93难度：0.9
解析
8．计算
8
+
18
的结果是
．
组卷：153引用：4难度：0.7
解析
9．关于x的方程x²+px+q=0的两个根分别为-1、4，则p+q的值为
．
组卷：703引用：9难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共11小题，共88分）

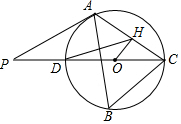26．如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．
（1）求证：PA是⊙O的切线；
（2）若OH⊥AC，OH=1，求DH的长．
组卷：804引用：3难度：0.5
解析
27．【提出问题】
（1）已知点P是⊙O外的一点，在⊙O上找一点A，使P、A两点间距离最短．
如图①，连接OP，OP与⊙O的交点A即为所求，此时线段PA最短．为了证明点A即为所求，不妨在⊙O上另外任取一点B，连接PB，OB，证明PB＞PA．请完成这个证明．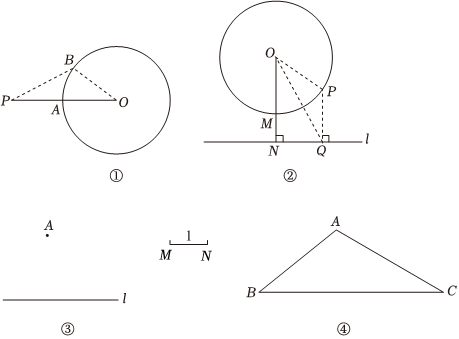

【变式探究】
（2）已知直线l与⊙O相离，在⊙O上找一点M，使点M到直线l的距离最短．
小明给出下列解答，请你补全小明的解答．
小明的解答
如图②，过点O作ON⊥l,垂足为N，ON与⊙O的交点M即为所求，此时线段MN最短．为了证明点M即为所求，不妨在⊙O上另外任取一点P，过点P作PQ⊥l,垂足为Q，连接OP，OQ，即证明PQ＞MN．
∵
，OQ＞ON，∴OP+PQ＞ON．
又
，∴OP+PQ＞OM+MN．
又OP=OM，∴PQ＞MN．
【拓展研究】
（3）如图③，已知直线l和直线外一点A，线段MN的长度为1．请用直尺和圆规作出一个⊙O，使⊙O经过点A，且⊙O上的点到直线l的距离的最小值为1．（不写作法，保留作图痕迹）
（4）如图④，在△ABC中，AC=8，BC=12，∠C=30°，⊙O经过点A，且⊙O上的点到直线BC的距离的最小值为2，距离最小值为2时所对应的⊙O上的点记为点P，若点P在△ABC的内部（不包括边界），则⊙O的半径r的取值范围是
．
组卷：60引用：2难度：0.3
解析