【提出问题】
（1）已知点P是⊙O外的一点，在⊙O上找一点A，使P、A两点间距离最短．
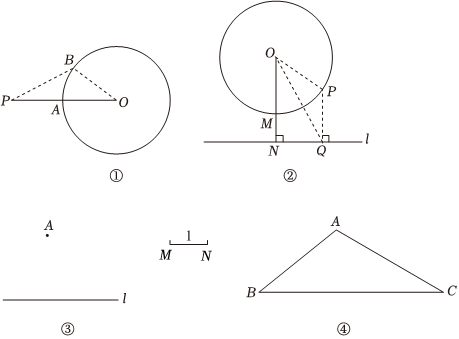
如图①，连接OP，OP与⊙O的交点A即为所求，此时线段PA最短．为了证明点A即为所求，不妨在⊙O上另外任取一点B，连接PB，OB，证明PB＞PA．请完成这个证明．
【变式探究】
（2）已知直线l与⊙O相离，在⊙O上找一点M，使点M到直线l的距离最短．
小明给出下列解答，请你补全小明的解答．
小明的解答
如图②，过点O作ON⊥l,垂足为N，ON与⊙O的交点M即为所求，此时线段MN最短．为了证明点M即为所求，不妨在⊙O上另外任取一点P，过点P作PQ⊥l,垂足为Q，连接OP，OQ，即证明PQ＞MN．
∵OP+PQ＞OQOP+PQ＞OQ，OQ＞ON，∴OP+PQ＞ON．
又 ON=OM+MNON=OM+MN，∴OP+PQ＞OM+MN．
又OP=OM，∴PQ＞MN．
【拓展研究】
（3）如图③，已知直线l和直线外一点A，线段MN的长度为1．请用直尺和圆规作出一个⊙O，使⊙O经过点A，且⊙O上的点到直线l的距离的最小值为1．（不写作法，保留作图痕迹）
（4）如图④，在△ABC中，AC=8，BC=12，∠C=30°，⊙O经过点A，且⊙O上的点到直线BC的距离的最小值为2，距离最小值为2时所对应的⊙O上的点记为点P，若点P在△ABC的内部（不包括边界），则⊙O的半径r的取值范围是 1＜r＜41＜r＜4．
【考点】圆的综合题．
【答案】OP+PQ＞OQ；ON=OM+MN；1＜r＜4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/1 8:0:8组卷：61引用：2难度：0.3
相似题
-
1．如图，已知⊙O的半径为1，P是平面内一点．
（1）如图①，若OP=2，过点P作⊙O的两条切线PE、PF，切点分别为E、F，连接EF．则∠EPO=°，EF=．
（2）若点M、N是⊙O上两点，且存在∠MPN=90°，则规定点P为⊙O的“直角点”．
①如图②，已知平面内有一点D，OD=，试说明点D是⊙O的“直角点”．2
②如图③，直线y=x-2分别与x轴、y轴相交于点A、B，若线段AB上所有点都是半径为r的圆的“直角点”，求r的最小值与该圆心的坐标．23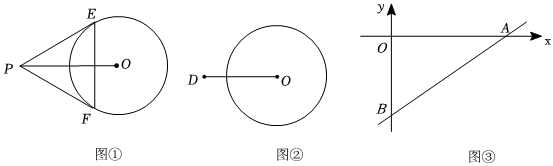
发布：2025/6/10 0:0:1组卷：215引用：1难度：0.5 -
2．对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离”，记作d（M，N）．特殊地，当图形M与图形N有公共点时，规定d（M，N）=0．
已知点A（-2，0），B（0，2），C（2，0），D（0，m）．3
（1）①求d（点O，线段AB）；
②若d（线段CD，直线AB）=1，直接写出m的值；
（2）⊙O的半径为r,若d（⊙O，线段AB）≤1，直接写出r的取值范围；
（3）若直线y=x+b上存在点E，使d（E，△ABC）＜=1，直接写出b的取值范围．3发布：2025/6/10 1:30:1组卷：525引用：2难度：0.1 -
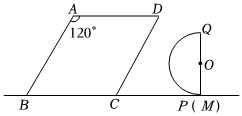3．如图，在菱形ABCD中，∠A=120°，AB=6，在直线BC上有一点M，CM=5，PQ=4，以PQ为直径的半圆O与直线BC相切于点P，点N为半圆弧PQ上一动点．
（1）当点P与点M重合时，H为半圆O上一点，则线段CH的最小值为 ；
（2）半圆O从点M出发沿MB做平移运动，速度为每秒1个单位长度，同时点N从点P开始绕圆心顺时针旋转，速度为每秒15°，设运动时间为t秒（0≤t≤11），解决下列问题：
①当t=2时，求此时点O到CD的距离及扇形ONP的面积；
②当半圆O与菱形ABCD有交点时，直接写出运动时间t的取值范围．发布：2025/6/10 0:30:1组卷：43引用：2难度：0.3
