2022-2023学年四川省绵阳市三台县高二（下）期中数学试卷（文科）

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．命题“∃x₀∈R，2^x₀＞

  x

  2

  0

  ”的否定是（　　）

  A．∀x∈R，2x＞x2	B．∃x0∈R，2x0≤ x 2 0
  C．∀x∈R，2x≤x2	D．∃x0∉R，2x0≤ x 2 0
  组卷：40引用：4难度：0.7

  解析

• 2．命题“若a+b=0，则a=0或b=0”的否命题是（　　）

  A．若a+b≠0，则a≠0或b≠0	B．若a+b≠0，则a≠0且b≠0
  C．若a≠0且b≠0，则a+b≠0	D．若a≠0或b≠0，则a+b≠0
  组卷：77引用：3难度：0.7

  解析

• 3．已知平面向量

  a

  =

  （

  1

  ，

  m

  ）

  ，

  b

  =

  （

  -

  4

  ，

  m

  ）

  ，则“m=2”是“

  a

  ⊥

  b

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：18引用：2难度：0.8

  解析

• 4．函数f（x）=xlnx在点（1，f（1））处切线方程为（　　）

  A．x-y-1=0

  B．x-y+1=0

  C．x+y-1=0

  D．x+y+1=0
  组卷：206引用：4难度：0.8

  解析

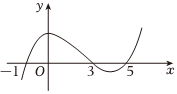• 5．定义在R上的函数f（x）的导函数为f'（x），如图是f'（x）的图像，下列说法中不正确的是（　　）

  A．[-1，3]为函数f（x）的单调增区间

  B．[3，5]为函数f（x）的单调减区间

  C．函数f（x）在x=0处取得极大值

  D．函数f（x）在x=5处取得极小值
  组卷：113引用：5难度：0.7

  解析

• 6．直线l：y=2x+1与曲线C：

  x = 2 cosα

  y = 3 sinα

  （α为参数）的位置关系为（　　）

  A．相交

  B．相切

  C．相离

  D．相交或相离
  组卷：29引用：2难度：0.5

  解析

• 7．若函数f（x）=lnx+2x²+bx+1的图像上任意一点的切线的斜率都大于0，则实数b的取值范围为（　　）

  A．（-∞，-4）

  B．（-∞，4）

  C．（-4，+∞）

  D．（4，+∞）
  组卷：17引用：1难度：0.5

  解析

三、解答题：本大题共6个小题，其中第17题10分，其余每小题10分，共70分，解答应写出文字说明，证明过程或演算步骤。

• 21．已知函数f（x）=

  1

  3

  x³+x²+ax.
  （1）若函数f（x）在区间（-2，+∞）上单调递增，求实数a的取值范围；
  （2）若函数g（x）=

  x

  e

  x

  ，对∀x₁∈[

  1

  2

  ，1]，∃x₂∈[

  1

  2

  ，2]，使得f'（x₁）≤g（x₂）成立，求实数a的取值范围．
  组卷：95引用：4难度：0.5

  解析

• 22．已知函数f（x）=ax+lnx.
  （1）讨论函数f（x）的单调区间；
  （2）当a=-1时，函数g（x）=f（x）+e^xcosx-lnx-m在

  [

  0

  ，

  π

  2

  ]

  上的最大值为0，求实数m的值．
  组卷：14引用：3难度：0.5

  解析