2022-2023学年北京市房山区高一（下）期末数学试卷

一、选择题。共10小题，每小题5分，共50分。在每小题列出的四个选项中，选出符合题目要求的一项。

• 1．若角α的终边经过点P（1，-2），则sinα=（　　）

  A． 5 5

  B．- 2 5 5

  C．-2

  D．- 1 2
  组卷：292引用：6难度：0.7

  解析

• 2．在△ABC中，已知a=2，b=3，C=60°，则c等于（　　）

  A． 7

  B．7

  C． 19

  D．19
  组卷：277引用：5难度：0.9

  解析

• 3．下列命题中，正确的是（　　）

  A．一条直线和一个点确定一个平面

  B．两个平面相交，可以只有一个公共点

  C．三角形是平面图形

  D．四边形是平面图形
  组卷：206引用：2难度：0.7

  解析

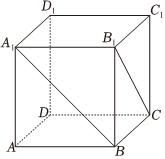• 4．在正方体ABCD-A₁B₁C₁D₁中，异面直线A₁B，B₁C所成角的大小为（　　）
  ​

  A．90°

  B．60°

  C．45°

  D．30°
  组卷：395引用：4难度：0.5

  解析

• 5．如图，在正四棱台ABCD-A₁B₁C₁D₁中，O₁，O分别为上、下底面中心，E₁，E分别为B₁C₁，BC的中点，则下列结论中错误的是（　　）

  A．O1OCC1是直角梯形	B．E1ECC1是直角梯形
  C．直线AD与直线B1B异面	D．直线O1O与直线B1B异面
  组卷：148引用：2难度：0.5

  解析

• 6．已知平面直角坐标系中的3点A（2，2），B（6，0），C（0，0），则△ABC中最大角的余弦值等于（　　）

  A． - 2 2

  B． 2 2

  C． - 10 10

  D． 10 10
  组卷：168引用：3难度：0.7

  解析

• 7．在三棱锥V-ABC中，VA，VB，VC两两垂直，VA=VB=VC=1，则点V到平面ABC的距离等于（　　）

  A．1

  B． 1 2

  C． 3

  D． 3 3
  组卷：105引用：2难度：0.6

  解析

三、解答题。共5小题，共70分。解答应写出文字说明，演算步骤或证明过程。

• 20．如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，M为AD的中点．
  （1）求证：PM⊥BC；
  （2）求证：平面PAB⊥平面PCD；
  （3）在棱PA上是否存在一点N，使得PC∥平面BMN？若存在，求

  AN

  NP

  的值；若不存在，请说明理由．
  组卷：471引用：3难度：0.5

  解析

• 21．某城市计划新修一座城市运动主题公园，该主题公园为平面五边形ABCDE（如图所示），其中三角形ABE区域为儿童活动场所，三角形BCD区域为文艺活动场所，三角形BDE区域为球类活动场所，AB，BC，CD，DE，EA为运动小道（不考虑宽度），∠BCD=∠BAE=120°，

  BC

  =

  CD

  =

  2

  3

  km

  ，DE=8km.
  （1）求BD的长度；
  （2）再从条件①、条件②这两个条件中选择一个作为已知，求BE的长度；
  （3）在（2）的条件下，应该如何设计，才能使儿童活动场所（即三角形ABE）的面积最大？
  条件①：

  cos

  ∠

  DBE

  =

  3

  5

  ；
  条件②：∠CDE=120°．
  注：如果选择条件①和条件②分别解答，按第一个解答计分．
  组卷：102引用：2难度：0.6

  解析