2022-2023学年吉林省白城市洮南一中高二（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．数列

  3

  5

  ，

  4

  7

  ，

  5

  9

  ，

  6

  11

  ，…，则该数列的第n项为（　　）

  A． n 2 n - 1

  B． n + 2 2 n - 3

  C． n 2 n + 1

  D． n + 2 2 n + 3
  组卷：592引用：7难度：0.8

  解析

• 2．设f（x）为可导函数，且满足

  lim

  Δ

  x

  →

  0

  f

  （

  1

  +

  3

  Δ

  x

  ）

  -

  f

  （

  1

  ）

  Δ

  x

  =

  -

  3

  ，则函数y=f（x）在x=1处的导数为（　　）

  A．-1	B．1
  C．1或-1	D．以上答案都不对
  组卷：38引用：4难度：0.8

  解析

• 3．已知函数f（x）=lnx+2xf′（1），则f（e）=（　　）

  A．1+2e

  B．1十e

  C．1-e

  D．1-2e
  组卷：135引用：4难度：0.7

  解析

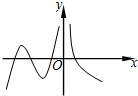• 4．已知函数y=f（x）的图象如图所示，则其导函数y=f′（x）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1098引用：18难度：0.9

  解析

• 5．设等差数列{a_n}的前n项和为S_n，且a₃+a₉=a₄+4，则S₁₅=（　　）

  A．45

  B．50

  C．60

  D．80
  组卷：137引用：3难度：0.7

  解析

• 6．已知P（x,y）是函数y=e^x+x图象上的点，则点P到直线2x-y-3=0的最小距离为（　　）

  A． 5 5

  B． 2 5 5

  C． 3 5 5

  D． 4 5 5
  组卷：88引用：6难度：0.9

  解析

• 7．公元前四世纪，毕达哥拉斯学派对数和形的关系进行了研究，他们借助几何图形（或格点）来表示数，称为形数，形数是联系算数和几何的纽带；如图为五角形数的前4个，现有如下说法：
  ①记所有的五角形数从小到大构成数列{a_n}，则a_n+1=a_n+3n+1；
  ②第9个五角形数比第8个五角形数多25；
  ③前8个五角形数之和为288；
  ④记所有的五角形数从小到大构成数列{a_n}，则{

  a

  n

  n

  }的前20项和为610．
  则正确的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：23引用：2难度：0.6

  解析

四、解答题：本题共6小题，共70分。

• 21．已知函数

  f

  （

  x

  ）

  =

  x

  2

  a

  -

  2

  lnx

  （

  a

  ∈

  R

  ，

  a

  ≠

  0

  ）

  ．
  （1）讨论函数f（x）的单调性；
  （2）若函数f（x）有最小值，记为g（a），关于a的方程

  g

  （

  a

  ）

  +

  a

  -

  2

  9

  a

  -

  1

  =

  m

  有三个不同的实数根，求实数m的取值范围．
  组卷：146引用：2难度：0.5

  解析

• 22．已知函数f（x）=

  a

  e

  x

  +sinx（a∈R，e为自然对数的底数）．
  （1）当a=1且x∈（-∞，0]时，求f（x）的最小值；
  （2）若函数f（x）在（-

  π

  2

  ，0）上存在极值点，求实数a的取值范围．
  组卷：22引用：1难度：0.4

  解析