2023-2024学年河南省焦作市博爱一中高三（上）月考数学试卷（8月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知A={1，x,y}，B={1，x²，2y}，若A=B，则x-y=（　　）

  A．2

  B．1

  C． 1 4

  D． 3 2
  组卷：1048引用：17难度：0.7

  解析

• 2．已知函数f（x）是R上的奇函数，且f（x+3）=-f（x），且当

  x

  ∈

  （

  0

  ，

  3

  2

  ]

  时，f（x）=2x-1，则f（-2021）+f（2022）的值是（　　）

  A．1

  B．-1

  C．0

  D．-3
  组卷：116引用：6难度：0.7

  解析

• 3．已知点

  P

  （

  cos

  π

  3

  ，

  1

  ）

  是角α终边上一点，则sinα=（　　）

  A． 5 5

  B． 3 2

  C． 1 2

  D． 2 5 5
  组卷：405引用：8难度：0.7

  解析

• 4．在四面体O-ABC中，点M在OA上，且OM=2MA，N为BC的中点，若

  OG

  =

  1

  3

  OA

  +

  x

  4

  OB

  +

  x

  4

  OC

  ，则使G与M，N共线的x的值为（　　）

  A．1

  B．2

  C． 2 3

  D． 4 3
  组卷：729引用：9难度：0.9

  解析

• 5．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥侧面积的一半，那么其侧面三角形底边上的高与底面正方形的边长的比值为（　　）

  A． 2 - 1 4

  B． 2 - 1 2

  C． 2 + 1 4

  D． 2 + 1 2
  组卷：628引用：10难度：0.7

  解析

• 6．某大街在甲、乙、丙三处设有红绿灯，汽车在这三处遇到绿灯的概率分别是

  1

  3

  ，

  1

  2

  ，

  2

  3

  ，则汽车在这三处共遇到两次绿灯的概率为（　　）

  A． 1 9

  B． 1 6

  C． 1 3

  D． 7 18
  组卷：221引用：6难度：0.7

  解析

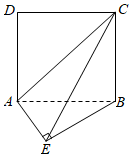• 7．如图所示，在直二面角D-AB-E中，四边形ABCD是边长为2的正方形，△AEB是等腰直角三角形，其中∠AEB=90°，则点D到平面ACE的距离为（　　）

  A． 3 3

  B． 2 3 3

  C． 3

  D．2 3
  组卷：209引用：11难度：0.7

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．规定

  C

  m

  x

  =

  x

  （

  x

  -

  1

  ）

  …

  （

  x

  -

  m

  +

  1

  ）

  m

  !

  ，其中x∈R，m∈N，且

  C

  0

  x

  =

  1

  ，这是组合数

  C

  m

  n

  （n,m∈N，且m≤n）的一种推广．
  （1）求

  C

  3

  -

  7

  的值．
  （2）组合数具有两个性质：①

  C

  m

  n

  =

  C

  n

  -

  m

  n

  ；②

  C

  m

  n

  +

  C

  m

  +

  1

  n

  =

  C

  m

  +

  1

  n

  +

  1

  ．这两个性质是否都能推广到

  C

  m

  x

  （x∈R，m∈N）？若能，请写出推广的形式并给出证明；若不能，请说明理由．
  组卷：44引用：3难度：0.6

  解析

• 22．已知椭圆C的中心为坐标原点，对称轴为x轴，y轴，且过

  （

  2

  ，

  0

  ）

  ，

  （

  3

  ，

  3

  2

  ）

  两点．
  （1）求椭圆C的方程；
  （2）是否存在直线l,使得直线l与圆x²+y²=1相切，与椭圆C交于A，B两点，且满足

  OA

  •

  OB

  =

  0

  （O为坐标原点）？若存在，请求出直线l的方程，若不存在，请说明理由．
  组卷：122引用：7难度：0.2

  解析