当前位置：试卷中心 > 试卷详情

2022-2023学年广东省深圳市南山区桃源中学八年级（上）第一次月考数学试卷

发布：2024/6/12 8:0:8

1．一个三角形的两边长分别是3和7，且第三边长为整数，这样的三角形周长最大的值为（　　）
A．15 B．16 C．18 D．19
组卷：624引用：17难度：0.9
解析
2．画△ABC中AB边上的高，下列画法中正确的是（　　）
A． B． C． D．
组卷：4306引用：62难度：0.9
解析
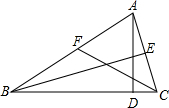3．如图，AD，BE，CF依次是△ABC的高、中线和角平分线，下列表达式中错误的是（　　）
A．AE=CE B．∠ADC=90° C．∠CAD=∠CBE D．∠ACB=2∠ACF
组卷：688引用：7难度：0.9
解析
4．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S_△ABC=4cm²，则S_阴影等于（　　）
A．2cm² B．1cm² C．
1
2
cm² D．
1
4
cm²
组卷：2556引用：86难度：0.9
解析
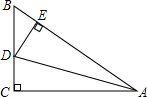5．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④AD平分∠CDE；⑤S_△ABD：S_△ACD=AB：AC，其中正确的有（　　）
A．5个 B．4个 C．3个 D．2个
组卷：3601引用：25难度：0.5
解析

6．下列说法中错误的是（　　）

A．三角形的三个内角中至少有两个角是锐角

B．有一个角是锐角的三角形是锐角三角形

C．一个三角形的三个内角中至少有一个内角不大于60°

D．如果三角形的两个内角之和小于90°，那么这个三角形是钝角三角形

组卷：181引用：3难度：0.7

7．一个多边形少算一个内角，其余内角之和是1500°，则这个多边形的边数是（　　）
A．8 B．9 C．10 D．11
组卷：499引用：7难度：0.9
解析
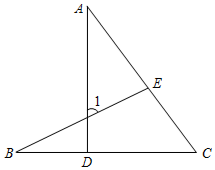8．如图，点D、E分别在线段BC、AC上，连接AD、BE．若∠A=35°，∠B=25°，∠C=50°，则∠1的大小为（　　）
A．60° B．70° C．75° D．85°
组卷：2693引用：29难度：0.5
解析

23．如图，在△ABC中，点E是边AC上一点，∠AEB=∠ABC．
（1）如图1，作∠BAC的平分线交CB、BE于D、F两点．求证：∠EFD=∠ADC．
（2）如图2，作△ABC的外角∠BAG的平分线，交CB的延长线于点D，延长BE、DA交于点F，试探究（1）中的结论是否成立？请说明理由．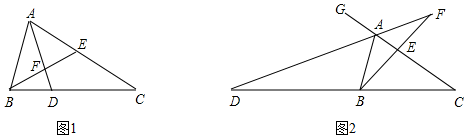
组卷：659引用：6难度：0.7
解析
24．已知，△ABC是等腰直角三角形，BC=AB，点A在x轴负半轴上，直角顶点B在y轴上，点C在x轴上方．

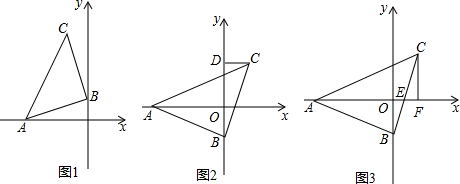
（1）如图1，若A的坐标是（-3，0），点B的坐标是（0，1），求点C的坐标；
（2）如图2，过点C作CD⊥y轴于D，请直接写出线段OA，OD，CD之间等量关系；
（3）如图3，若x轴恰好平分∠BAC，BC与x轴交于点E，过点C作CF⊥x轴于F，问CF与AE有怎样的数量关系？并说明理由．
组卷：2597引用：32难度：0.1
解析