2021-2022学年四川省成都市新都一中高一（下）期末数学模拟试卷（5）

一、单选题

• 1．等比数列{a_n}中，若a₅=9，则log₃a₄+log₃a₆=（　　）

  A．2

  B．3

  C．4

  D．9
  组卷：1013引用：21难度：0.8

  解析

• 2．已知直线a,b和平面α，β，若a⊂α，b⊂β，α⊥β，则下列情况不可能成立的是（　　）

  A．a∥b且a∥β

  B．a∥b且a⊥β

  C．a⊥b且a∥β

  D．a⊥b且a⊥β
  组卷：38引用：2难度：0.9

  解析

• 3．在△ABC中，角A、B、C所对的对边长分别为a、b、c,sinA、sinB、sinC成等比数列，且c=2a,则cosB的值为（　　）

  A． 1 4

  B． 3 4

  C． 2 4

  D． 2 3
  组卷：264引用：23难度：0.7

  解析

• 4．已知a,b为两条不同的直线，α为平面，则下列命题正确的是（　　）

  A．若a⊥α，a⊥b,则b∥α	B．若a∥α，a⊥b,则b⊥α
  C．若a∥α，b∥α，则a∥b	D．若a⊥α，a∥b,则b⊥α
  组卷：104引用：11难度：0.6

  解析

• 5．在正方体ABCD-A₁B₁C₁D₁中，M为棱CC₁的中点，则异面直线AM与C₁D₁所成角的正切值为（　　）

  A． 1 2

  B． 1 3

  C． 5 2

  D． 7 2
  组卷：16引用：1难度：0.6

  解析

• 6．计算

  1

  +

  tan

  7

  12

  π

  1

  -

  tan

  7

  12

  π

  =（　　）

  A． - 3 3

  B． 3 3

  C． - 3

  D． 3
  组卷：257引用：3难度：0.7

  解析

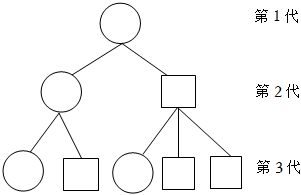• 7．自然界的一些生物具有特殊的增殖方式，某种细菌有A和B两种类型，A型个体每次增殖得到1个A型和1个B型的子代，B型个体每次增殖得到1个A型和2个B型的子代．如图所示（A型个体用圆圈表示，B型个体用方框表示），若以1个A型细菌个体为第1代，则第8代细菌个体的总数量为（　　）

  A．477

  B．521

  C．610

  D．687
  组卷：7引用：3难度：0.8

  解析

三、解答题

• 21．已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD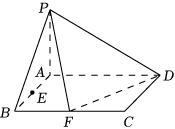，E、F分别是线段AB、BC的中点．
  （1）证明：PF⊥FD；
  （2）在线段PA上是否存在点G，使得EG∥平面PFD，若存在，确定点G的位置；若不存在，说明理由．
  组卷：593引用：6难度：0.1

  解析

• 22．已知数列{a_n}的前n项和为S_n，a₁=1且2nS_n+1-2（n+1）S_n=n（n+1），数列{b_n}前n项和P_n，且满足

  P

  n

  =

  2

  •

  3

  n

  -

  1

  -

  2

  3

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）求数列{a_n}，{b_n}的通项公式a_n和b_n；
  （2）求数列{a_nb_n}的前n项的和M_n；
  （3）令

  c

  n

  =

  a

  n

  +

  2

  a

  n

  +

  a

  n

  a

  n

  +

  2

  ，记{c_n}的前n项和为T_n，对∀n∈N^*，均有T_n-2n∈[a,b]，求b-a的最小值．
  组卷：140引用：2难度：0.4

  解析