2023-2024学年山西省大同市、阳泉市多校九年级（上）联考数学试卷（9月份）

一、选择题（本大题共10个小题，每小题3分，共30分.在每个小题

• 1．一元二次方程x²-3=0的解为（　　）

  A．x1=x2= 3

  B．x1= 3 ，x2=- 3

  C．x1=x2=9

  D．x1=9，x2=-9
  组卷：47引用：2难度：0.7

  解析

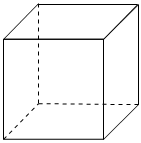• 2．如图，一个正方体的棱长为x cm,它的表面积为y cm²，则y与x的函数关系式为（　　）

  A．y=x2

  B．y=3x2

  C．y=6x2

  D．y=12x2
  组卷：343引用：2难度：0.5

  解析

• 3．将一元二次方程x（x+1）=4化为一般形式后，它的各项系数的和为（　　）

  A．6

  B．4

  C．2

  D．-2
  组卷：49引用：2难度：0.7

  解析

• 4．二次函数y=x²+8x+9的对称轴为直线（　　）

  A．x=4

  B．x=-4

  C． x = - 1 4

  D． x = 1 4
  组卷：299引用：3难度：0.6

  解析

• 5．我们解一元二次方程（x-3）²-5（x-3）=0时，可以运用因式分解法将此方程化为（x-3）（x-3-5）=0．从而得到两个一元一次方程：x-3=0或x-8=0．进而得到原方程的解为x₁=3，x₂=8，这种解法体现的数学思想是（　　）

  A．数形结合思想	B．函数思想
  C．公理化思想	D．转化思想
  组卷：41引用：1难度：0.7

  解析

• 6．一元二次方程x²-6x+1=0根的情况为（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．无法判断其根的情况
  组卷：78引用：2难度：0.5

  解析

• 7．将抛物线y=x²-2向右平移3个单位长度，再向下平移1个单位长度，得到的抛物线的解析式为（　　）

  A．y=（x+3）2-3

  B．y=（x+3）2+3

  C．y=（x-3）2+3

  D．y=（x-3）2-3
  组卷：157引用：2难度：0.5

  解析

三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

• 22．综合与实践
  【项目学习】
  配方法是数学中重要的一种思想方法，利用配方法可求一元二次方程的根，也可以求二次函数的顶点坐标等．所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．其实这种方法还经常被用到代数式的变形中，并结合非负数的意义解决某些问题．
  例1：把代数式x²+8x+25进行配方．
  解：原式=x²+8x+16+9=（x+4）²+9．
  例2：求代数式-x²+4x-7的最大值．
  解：原式=-（x²-4x+4）-3=-（x-2）²-3．∵（x-2）²≥0，∴-（x-2）²≤0，∴-（x-2）²-3≤-3，∴-x²+4x-7的最大值为-3．
  【问题解决】
  （1）若m,k,h满足2m²-12m+11=2（m-k）²+h,求k+h的值．
  （2）若等腰△ABC的三边长a,b,c均为整数，且满足a²+2b²-8a-20b=-66，求△ABC的周长．
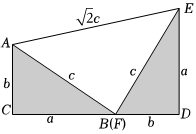
  （3）如图，这是美国总统加菲尔德证明勾股定理的一个图形，其中a,b,c是Rt△ABC和Rt△DEF的三边长，根据勾股定理可得AE=

  c

  2

  +

  c

  2

  =

  2

  c,我们把关于x的一元二次方程ax²+

  2

  cx+b=0称为“勾系一元二次方程”．已知实数p,q满足等式q-p²+15p-48=0，且p+q的最小值是“勾系一元二次方程”ax²+

  2

  cx+b=0的一个根．四边形ACDE的周长为6

  2

  ，试求△ABC的面积．
  组卷：232引用：1难度：0.7

  解析

• 23．综合与探究
  如图1，已知抛物线y=x²+bx+c与x轴相交于点A（-3，0），B（1，0），与y轴交于点C．
  （1）求抛物线y=x²+bx+c及直线AC的函数表达式．
  （2）如图2，P是直线AC下方的抛物线上的一点，过点P作PQ⊥x轴于点Q，交直线AC于点D，当

  S

  △

  CQD

  S

  △

  CPD

  =

  1

  2

  时，求点P的坐标．
  （3）如图3，过点O作OM⊥AC于点M，将线段OM所在的直线沿着x轴平移，使得平移后的直线交x轴于点E，交抛物线于点F，是否存在点F，使得四边形OMEF是平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．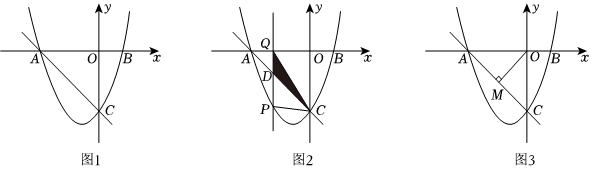
  组卷：99引用：1难度：0.3

  解析