综合与实践
【项目学习】
配方法是数学中重要的一种思想方法，利用配方法可求一元二次方程的根，也可以求二次函数的顶点坐标等．所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．其实这种方法还经常被用到代数式的变形中，并结合非负数的意义解决某些问题．
例1：把代数式x²+8x+25进行配方．
解：原式=x²+8x+16+9=（x+4）²+9．
例2：求代数式-x²+4x-7的最大值．
解：原式=-（x²-4x+4）-3=-（x-2）²-3．∵（x-2）²≥0，∴-（x-2）²≤0，∴-（x-2）²-3≤-3，∴-x²+4x-7的最大值为-3．
【问题解决】
（1）若m,k,h满足2m²-12m+11=2（m-k）²+h,求k+h的值．
（2）若等腰△ABC的三边长a,b,c均为整数，且满足a²+2b²-8a-20b=-66，求△ABC的周长．
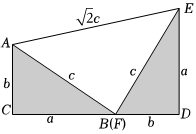
（3）如图，这是美国总统加菲尔德证明勾股定理的一个图形，其中a,b,c是Rt△ABC和Rt△DEF的三边长，根据勾股定理可得AE=

c

2

+

c

2

=

2

c,我们把关于x的一元二次方程ax²+

2

cx+b=0称为“勾系一元二次方程”．已知实数p,q满足等式q-p²+15p-48=0，且p+q的最小值是“勾系一元二次方程”ax²+

2

cx+b=0的一个根．四边形ACDE的周长为6

2

，试求△ABC的面积．