2023年河北省衡水二中高考数学三模试卷
发布:2024/5/24 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知全集I={x∈N|x≤10},集合M={1,2,3},N={2,4,6,8,10},则∁I(M∪N)=( )
组卷:313引用:4难度:0.7 -
2.已知复数z=2+i,且
,其中a,b为实数,则( )az-z+b=0组卷:77引用:5难度:0.8 -
3.已知向量
,a满足b,|a|=2|b|=2,则(a-b)•(2a+b)=8与a的夹角为( )b组卷:164引用:5难度:0.7 -
4.在正方体ABCD-A1B1C1D1中,M是线段C1D1(不含端点)上的动点,N为BC的中点,则( )
组卷:175引用:5难度:0.6 -
5.第19届亚运会将于2023年9月在杭州举行,在杭州亚运会三馆(杭州奥体中心主体育馆、游泳馆和综合训练馆)对外免费开放预约期间,甲、乙、丙、丁4人预约参观,且每人预约了1个或2个馆,则这4人中每个馆恰有2人预约的不同方案有( )
组卷:196引用:3难度:0.5 -
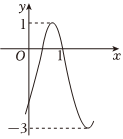 6.函数的部分图象如图所示,则f(x)=2sin(ωx-π6)+m(0<ω<4)=( )f(20233)组卷:96引用:2难度:0.7
6.函数的部分图象如图所示,则f(x)=2sin(ωx-π6)+m(0<ω<4)=( )f(20233)组卷:96引用:2难度:0.7 -
7.若
,a=10e10,b=10e-1则( )c=lg53组卷:48引用:2难度:0.5
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过点
,M(1,32).N(-23,263)
(1)求E的方程;
(2)已知P(2,0),是否存在过点G(-1,0)的直线l交E于A,B两点,使得直线PA,PB的斜率之和等于-1?若存在,求出l的方程;若不存在,请说明理由.组卷:120引用:4难度:0.4 -
22.已知函数
.f(x)=ex-e2x2-ax(a∈R)
(1)若f(x)在R上是增函数,求a的取值范围;
(2)若当时,f(x)有两个极值点m,n,证明:a∈(0,1e).f(m)-f(n)m-n<e-1组卷:124引用:3难度:0.6


