2023-2024学年广东省云浮市罗定中学城东学校高二(上)月考数学试卷(10月份)(1)
发布:2024/9/7 18:0:8
一、单选题(每小题5分,共40分.每个小题仅有一个答案是正确的)
-
1.若向量
,a=(1,1,0),则b=(-1,0,2)=( )|3a+b|组卷:325引用:4难度:0.7 -
2.已知向量
,a=(3,0,1),若b=(k,2,0)与a夹角为b,则k的值为( )π3组卷:25引用:3难度:0.7 -
3.已知向量
=(-2,3,-1),a=(4,m,n),且b∥a,其中m,n∈R,则m+n=( )b组卷:408引用:15难度:0.8 -
4.已知空间向量
,a=(2,0,1),b=(-1,2,1),若向量c=(0,4,z),a,b共面,则实数z=( )c组卷:156引用:5难度:0.5 -
5.在正方体ABCD-A1B1C1D1中,E是C1D1的中点,则异面直线DE与AC所成角的余弦值为( )
组卷:190引用:9难度:0.6 -
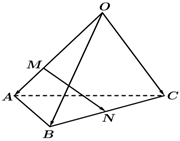 6.如图所示,在四面体O-ABC中,,OA=a,OB=b,点M在OA上,且OC=c=2OM,N为BC的中点,则MA=( )MN组卷:1253引用:41难度:0.9
6.如图所示,在四面体O-ABC中,,OA=a,OB=b,点M在OA上,且OC=c=2OM,N为BC的中点,则MA=( )MN组卷:1253引用:41难度:0.9 -
7.下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是( )
组卷:72引用:5难度:0.7
四、解答题:本大题共6小题,共70分.
-
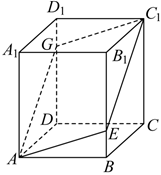 21.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,DD1=3,,G为棱DD1上一点,DG=2,过A,G,C1三点的平面α交BB1于点E.∠ABC=2π3
21.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,DD1=3,,G为棱DD1上一点,DG=2,过A,G,C1三点的平面α交BB1于点E.∠ABC=2π3
(1)求点D到平面BC1G的距离;
(2)求平面AEC与平面BEC所成锐二面角的余弦值.组卷:158引用:3难度:0.5 -
22.如图1,已知ABFE是直角梯形,EF∥AB,∠ABF=90°,∠BAE=60°,C、D分别为BF、AE的中点,AB=5,EF=1,将直角梯形ABFE沿CD翻折,使得二面角F-DC-B的大小为60°,如图2所示,设N为BC的中点.

(1)证明:FN⊥AD;
(2)若M为AE上一点,且,则当λ为何值时,直线BM与平面ADE所成角的正弦值为AMAE=λ.5714组卷:359引用:10难度:0.4


