2022-2023学年山东省日照市校际联考高一(下)期末数学试卷
发布:2024/6/15 8:0:9
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.sin20°cos40°+cos20°sin40°=( )
组卷:270引用:7难度:0.9 -
2.在△ABC中,A为钝角,则点P(tanB,cosA)( )
组卷:634引用:3难度:0.9 -
3.已知C为线段AB上一点,且AC=2CB,若O为直线AB外一点,则( )
组卷:82引用:3难度:0.8 -
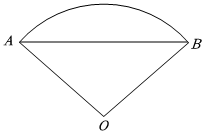 4.我国北宋时期科技史上的杰作《梦溪笔谈》收录了计算扇形弧长的近似计算公式:,公式中“弦”是指扇形中圆弧所对弦的长,“矢”是指圆弧所在圆的半径与圆心到弦的距离之差,“径”是指扇形所在圆的直径.如图,已知扇形的面积为lˆAB=弦+2×矢2径,扇形所在圆O的半径为2,利用上述公式,计算该扇形弧长的近似值为( )4π3组卷:409引用:7难度:0.7
4.我国北宋时期科技史上的杰作《梦溪笔谈》收录了计算扇形弧长的近似计算公式:,公式中“弦”是指扇形中圆弧所对弦的长,“矢”是指圆弧所在圆的半径与圆心到弦的距离之差,“径”是指扇形所在圆的直径.如图,已知扇形的面积为lˆAB=弦+2×矢2径,扇形所在圆O的半径为2,利用上述公式,计算该扇形弧长的近似值为( )4π3组卷:409引用:7难度:0.7 -
5.把函数y=sinx(x∈R)的图象上所有的点向左平行移动
个单位长度,再把所得图象上所有点的横坐标缩短到原来的π3(纵坐标不变),得到的图象所表示的函数是( )12组卷:297引用:5难度:0.9 -
6.已知函数
在区间f(x)=sin(ωx+π6)(ω>0)上单调递增,且存在唯一[-5π6,2π3]使得f(x0)=1,则ω的取值范围为( )x0∈[0,5π6]组卷:942引用:4难度:0.6 -
7.一个棱长为1分米的正方体形封闭容器中盛有V升水(没有盛满),若将该容器任意放置均不能使容器内水平面呈三角形,则V的一个可能取值为( )
组卷:21引用:1难度:0.5
四、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
-
 21.如图所示,在四棱锥P-ABCD中,底面四边形ABCD是平行四边形,且∠A=60°,AD=PD=2,AB=PB=4.
21.如图所示,在四棱锥P-ABCD中,底面四边形ABCD是平行四边形,且∠A=60°,AD=PD=2,AB=PB=4.
(1)证明:平面BCD⊥平面PAD;
(2)当二面角D-PA-B的平面角的余弦值为时,求直线BD与平面PBC夹角的正弦值.77组卷:138引用:1难度:0.5 -
 22.某烟花厂准备生产一款环保、安全的迷你小烟花,初步设计了一个平面图,如图所示,该平面图由Rt△ABF,直角梯形BCEF和以C为圆心的四分之一圆弧ED构成,其中AB⊥BF,BC⊥CE,BF∥CE,且BC=BF=1,CE=2,,将平面图形ADEF以AD所在直线为轴,旋转一周形成的几何体即为烟花.AB=72
22.某烟花厂准备生产一款环保、安全的迷你小烟花,初步设计了一个平面图,如图所示,该平面图由Rt△ABF,直角梯形BCEF和以C为圆心的四分之一圆弧ED构成,其中AB⊥BF,BC⊥CE,BF∥CE,且BC=BF=1,CE=2,,将平面图形ADEF以AD所在直线为轴,旋转一周形成的几何体即为烟花.AB=72
(1)求该烟花的体积;
(2)工厂准备将矩形PMNQ(该矩形内接于图形BDEF,M在弧DE上,N在线段EF上,PQ在AD上)旋转所形成的几何体用来安放燃料,设∠MCE=θ(),0<θ≤π3
①请用θ表示燃料的体积V;
②若烟花燃烧时间t和燃料体积V满足关系,请计算这个烟花燃烧的最长时间.t=V(9-7cosθ)cos2θ组卷:115引用:7难度:0.3


