2022-2023学年山东省青岛市九校联盟高二（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．空间直角坐标系中，已知A（-1，1，3），则点A关于平面xOz的对称点的坐标为（　　）

  A．（1，1，-3）

  B．（-1，-1，-3）

  C．（-1，1，-3）

  D．（-1，-1，3）
  组卷：71引用：6难度：0.8

  解析

• 2．若4名教师报名参加乡村志愿支教活动，可以从A，B，C这3个学校中选报1个，则不同的报名方式有（　　）

  A．16种

  B．24种

  C．64种

  D．81种
  组卷：50引用：1难度：0.8

  解析

• 3．质点M按规律s（t）=（2t-1）²做直线运动（位移单位：m,时间单位：s），则质点M在t=5s时的瞬时速度为（　　）

  A．16m/s

  B．36m/s

  C．64m/s

  D．81m/s
  组卷：65引用：1难度：0.8

  解析

• 4．抛物线x²=2y上一点A的纵坐标为2，则点A与抛物线焦点的距离为（　　）

  A． 3 2

  B．2

  C． 5 2

  D．3
  组卷：51引用：3难度：0.7

  解析

• 5．圆x²+y²-4x-4y-10=0上的点到直线x+y+6=0的最大距离是（　　）

  A． 2 2

  B． 4 2

  C． 8 2

  D． 16 2
  组卷：541引用：5难度：0.8

  解析

• 6．从8名女生和4名男生中，抽取3名学生参加某档电视节目，如果按性别比例分层抽样，则不同的抽取方法数为（　　）

  A．224

  B．112

  C．56

  D．28
  组卷：109引用：7难度：0.9

  解析

• 7．已知4a=ln4，b=e^-1，5c=ln5，则a,b,c的大小关系为（　　）

  A．a＞b＞c

  B．c＞a＞b

  C．b＞c＞a

  D．b＞a＞c
  组卷：157引用：3难度：0.6

  解析

四、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤。

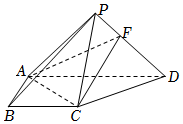• 21．如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=

  2

  ，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，

  PF

  =

  1

  2

  FD

  ．
  （1）求证：PB∥平面ACF；
  （2）在线段PB上是否存在一点H，使得CH与平面ACF所成角的正弦值为

  6

  6

  ？若存在，求出线段PH的长度；若不存在，请说明理由．
  组卷：253引用：5难度：0.5

  解析

• 22．已知函数f（x）=2（x-3）e^x-x+2lnx+5．
  （1）判断f（x）在

  （

  1

  2

  ，

  +

  ∞

  ）

  上的单调性；
  （2）若0＜x＜2，求证：

  f

  （

  x

  ）

  ＜

  -

  1

  2

  -

  2

  ln

  2

  ．
  组卷：89引用：3难度：0.5

  解析