当前位置：试卷中心 > 试卷详情

2022-2023学年贵州省贵阳市三新改革联盟校高一（下）联考数学试卷（5月份）

发布：2024/7/22 8:0:9

一、选择题：本题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．

1．i为虚数单位，若复数z=1+i,则|z|=（　　）
A．1 B．2 C．
2
D．
2
2
组卷：13引用：2难度：0.8
解析
2．已知
a
=
（
0
，
1
）
，
b
=
（
1
，
2
）
，
c
=
（
2
，
3
）
，则（　　）
A．
a
+
b
=
c
B．
a
+
c
=
2
b
C．
2
a
+
b
=
c
D．
a
+
2
b
=
c
组卷：89引用：2难度：0.8
解析
3．n棱柱（n∈N^*，n≥3）的顶点数为V，棱数为E，面数为F，则V+F-E=（　　）
A．-1 B．0 C．1 D．2
组卷：22引用：2难度：0.7
解析
4．等腰直角三角形的斜边为2，以斜边为轴旋转一周所得几何体的体积为（　　）
A．
π
3
B．
2
π
3
C．
2
π
3
D．
2
2
π
3
组卷：51引用：2难度：0.8
解析
5．在正方体ABCD-A₁B₁C₁D₁中，异面直线BD与B₁C所成角为（　　）
A．30° B．45° C．60° D．90°
组卷：85引用：3难度：0.7
解析
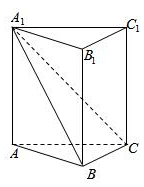6．如图，已知直三棱柱ABC-A₁B₁C₁，所有棱长均为2，则二面角A-BC-A₁的余弦值为（　　）
A．
1
3
B．
6
3
C．
21
7
D．
2
3
组卷：295引用：4难度：0.5
解析
7．在△ABC中，|AB|=5，|BC|=6，|AC|=7，则△ABC的面积是（　　）
A．
15
3
2
B．
6
6
C．12 D．
12
6
组卷：74引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．

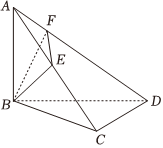21．如图，AB⊥平面BCD，BC⊥CD，BE⊥AC，垂足为E，BF⊥AD，垂足为F．
（1）求证：平面ABC⊥平面ACD；
（2）求证：AE•AC=AF•AD．
组卷：44引用：2难度：0.5
解析
22．材料1．类比是获取数学知识的重要思想之一，很多优美的数学结论就是利用类比思想获得的．例如：若a＞0，b＞0，则
a
+
b
2
≥
ab
，当且仅当a=b时，取等号，我们称为二元均值不等式．类比二元均值不等式得到三元均值不等式：a＞0，b＞0，c＞0，则
a
+
b
+
c
3
≥
3
abc
，当且仅当a=b=c时，取等号．我们经常用它们求相关代数式或几何问题的最值，某同学做下面几何问题就是用三元均值不等式圆满完成解答的．
题：将边长为12cm的正方形硬纸片（如图1）的四个角裁去四个相同的小正方形后，折成如图2的无盖长方体小纸盒，求纸盒容积的最大值．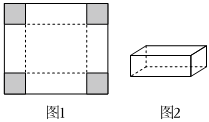

解：设截去的小正方形的边长为x（0＜x＜6），则纸盒容积V=（12-2x）²x=
1
4
（
12
-
2
x
）
（
12
-
2
x
）
（
4
x
）
≤
1
4
（
12
-
2
x
+
12
-
2
x
+
4
x
3
）
3
=128．
当且仅当12-2x=12-2x=4x,即x=2时取等号．所以纸金的容积取得最大值128cm³．在求V的最大值中，用均值不等式求最值时，遵循“一正二定三相等”的规则．你也可以将V=（12-2x）²x变形为V=（12-2x）²x=2（6-x）（6-x）（2x）求解．
你还可以设纸盒的底面边长为a,高为b,则a+2b=12，则纸盒容积V=a²b=
1
4
aa
（
4
b
）
≤
1
4
（
a
+
a
+
4
b
3
）
3
=
1
4
×
（
2
（
a
+
2
b
）
3
）
3
=
1
4
×
（
2
×
12
3
）
3
=128．
当且仅当a=a=4b,即a=8，b=2时取等号，所以纸盒的容积取得最大值128cm³．
材料2．《数学必修二》第八章8.3节习题8.3设置了如下第4题：
如图1，圆锥的底面直径和高均为a,过PO的中点O₁作平行于底面的截面，以该截面为底的面挖去一个圆柱，求剩下几何体的表面积和体积．我们称圆柱为圆锥的内接圆柱．
根据材料1与材料2完成下列问题．
如图2，底面直径和高均为6cm的圆锥有一个底面半径为R，高为H的内接圆柱．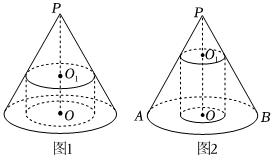

（1）求R与H的关系式；
（2）求圆柱侧面积的最大值；
（3）求圆柱体积的最大值．
组卷：69引用：2难度：0.5
解析